เลือกอ่านตามหัวข้อ?
เข้าหาบทความพี่ง่ายๆ จาก Google
เกริ่นนำ : อะไรคือฟังก์ชันผกผัน
หากน้องจำกันได้ ฟังก์ชันผกผัน (Inverse Function) ก็คือ สลับตัว X (สิ่งนำเข้า) และ Y (ผลลัพธ์) นั่นเอง หากใครลืมเรื่องฟังก์ชันผกผันสามารถกลับไปทวนกันก่อนได้ในเรื่องฟังก์ชันนะครับ ถ้าให้ Recap กันแบบเร็ว ๆ ก็คือหากเราวาดกราฟ เราจะพลิกกราฟ นำแกน X เป็น Y และแกน Y เป็น X
ดังนั้น ในเรื่องฟังก์ชันตรีโกณมิติ ก็ไม่มีอะไรแตกต่างครับน้อง หากพี่ยกตัวอย่าง \(y=\sin{x}\) เรารู้กันทันทีว่า ฟังก์ชันนี้ รับ มุม x เข้ามา และคืนค่ากลับ เป็นค่า sin ของมุมนั้น ๆ เช่นหากน้องเป็นฟังก์ชัน \(\sin(x)\) และพี่ ให้ค่า \(x\) น้องเป็น \(30^\circ\) น้องก็ต้องตอบพี่ว่า \(\dfrac{1}{2}\) ประมาณนี้
ดังนั้น ฟังก์ชันผกผันตรีโกณมิติก็จะแตกต่างกันแค่ สลับค่าที่ให้กับค่าที่ตอบ ตอนแรก น้องได้มุมและตอบค่าฟังก์ชัน แต่ในฟังก์ชันผกผัน น้องจะได้ค่าและต้องหาว่ามุมอะไร
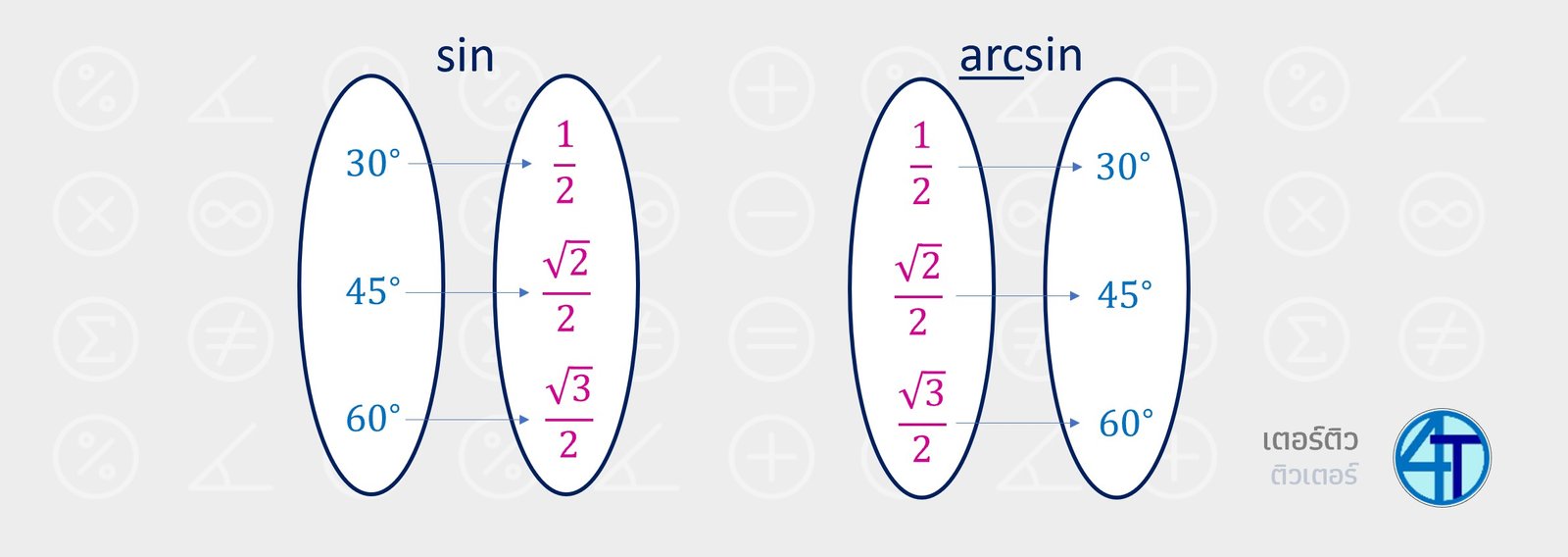
ยกตัวอย่างเพื่อความง่าย หากพี่ถามน้องว่า \(\sin\) อะไรได้ \(\dfrac{1}{2}\) น้องก็จะตอบพี่ว่า \(30^\circ\) ดังนั้น \(\textcolor{blue}{\text{arc}}\text{sin}\left(\dfrac{1}{2}\right)=30^\circ\) สังเกตที่พี่ใส่คำว่า arc เข้าไปด้านหน้า นี่แหละครับฟังก์ชันผกผันของ \(\sin\) ซึ่งสิ่งที่ฟังก์ชันได้ไม่ใช่มุมแต่เป็นค่า และฟังก์ชันนี้ต้องตอบว่า มุมอะไรนะ ที่ทำให้ \(\sin\) มีค่าเป็น \(\dfrac{1}{2}\)
แต่ก็มีหลายมุมที่ให้ค่าเท่ากัน...
หากน้องจำได้ \(\sin\) ที่ให้ค่า \(\dfrac{1}{2}\) ไม่ได้มีค่าเดียว ใช่ครับ เช่น \(\sin{150^\circ}\) หรือ \(\sin{390^\circ}\) ก็ล้วนแล้วแต่เป็น \(\dfrac{1}{2}\) ทั้งคู่ ดังนั้นแปลว่า \(\textcolor{blue}{\text{arc}}\text{sin}\left(\dfrac{1}{2}\right)=30^\circ\) หรือ \(150^\circ\) หรือ \(390^\circ\) อะไรก็ได้หรอ?
คำตอบ คือ ไม่ได้ครับน้อง เพราะหาก \(\arcsin\) สามารถให้คำตอบได้หลายค่า เราจะไม่เรียกมันว่าฟังก์ชัน การให้คำตอบหลายค่าก็เหมือนกับ ให้ \(x\) หนึ่งตัว แต่ค่า \(y\) ออกมาหลายตัว หรือที่เราเรียกว่า ความสัมพันธ์แบบ one-to-many นั่นเอง ซึ่งจากเรื่องฟังก์ชัน เราเรียนกันมาแล้วว่า one-to-many ไม่เป็นฟังก์ชัน ดังนั้น หากฟังก์ชันผกผันตรีโกณมิติ (\(\text{arc-}\)) สามารถคืนค่ามุมคำตอบได้หลายค่า มันจะไม่เป็นฟังก์ชัน แล้วเราจะแก้ปัญหานี้ยังไงหล่ะ?
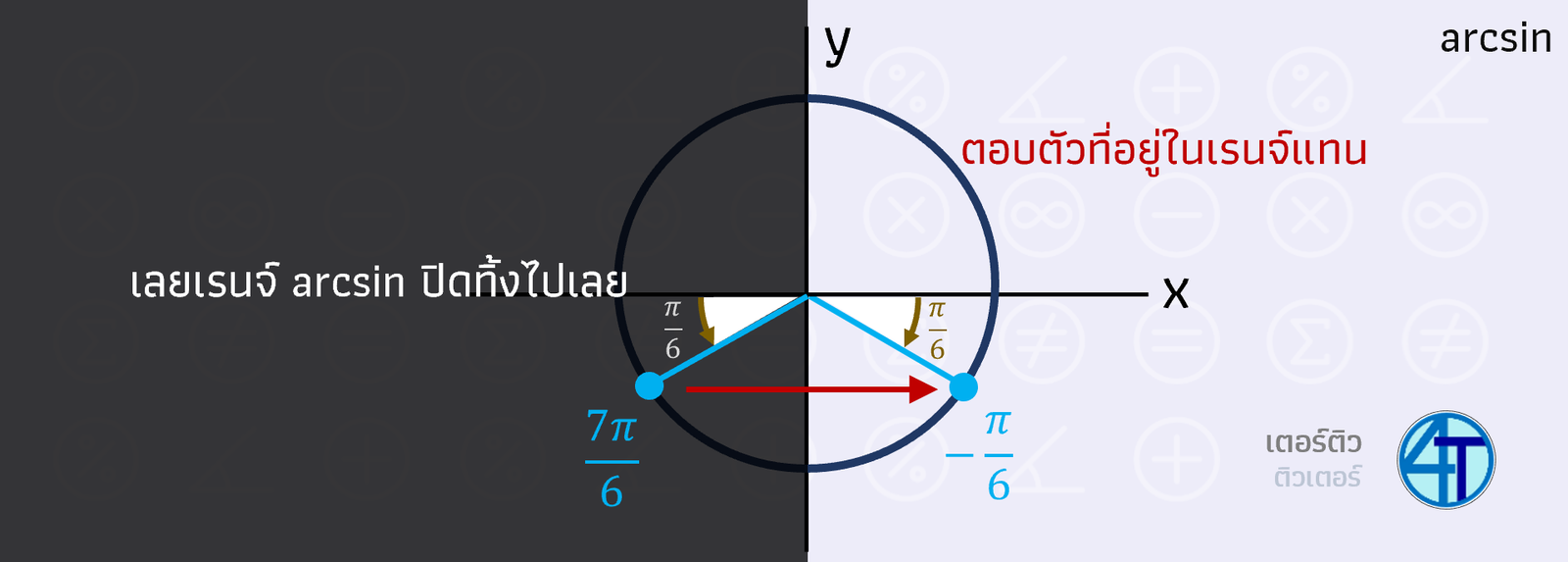
กำหนดเรนจ์ของฟังก์ชัน (ช่วงมุมคำตอบที่ตอบได้)
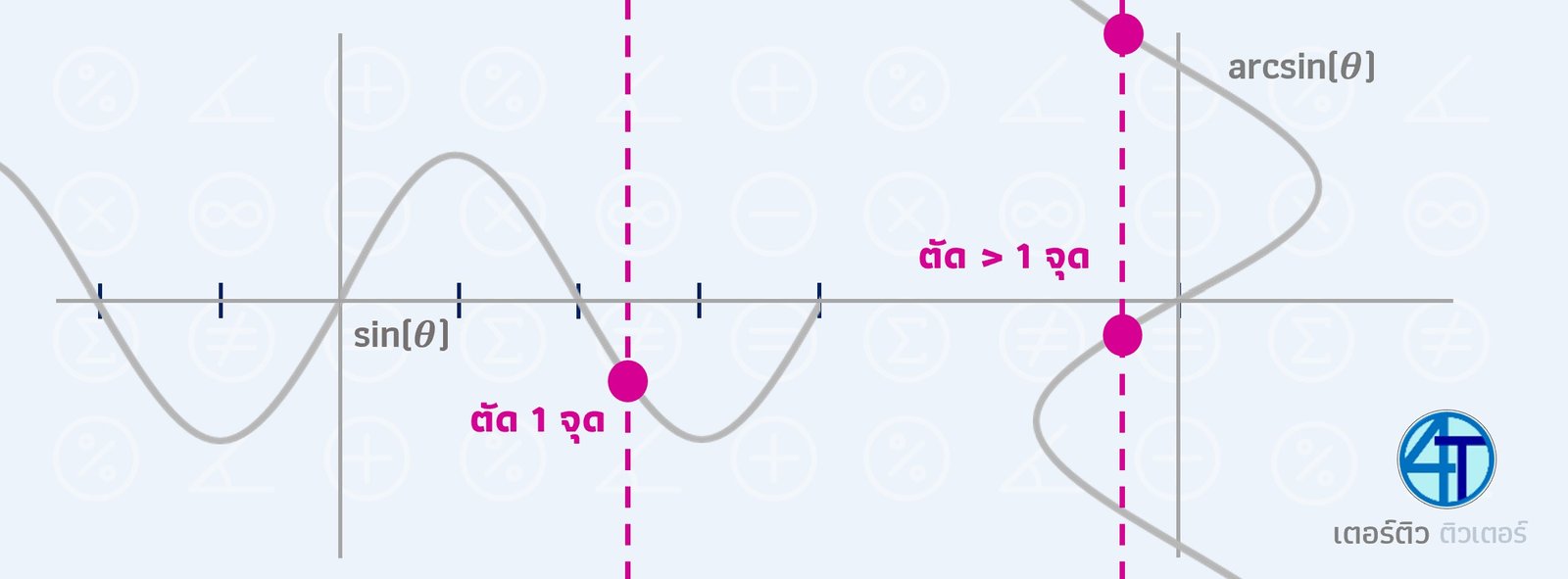
หากยังจำกันได้การเช็คว่ากราฟเป็นฟังก์ชันหรือไม่ คือการ ลากเส้นตรงตั้งฉากกับแกน X หากมีเส้นที่ลากโดนกราฟมากกว่า 1 ที กราฟนั้นไม่เป็นฟังก์ชัน มองง่าย ๆ (ตามภาพด้านบน) คือ การที่ลากเส้นแล้วตัดมากกว่า 1 จุดแปลว่า ที่ X หนึ่งตัว (input) กราฟมีค่า Y (output) มากกว่าหนึ่ง ก็ที่เราเรียกกันง่าย ๆ ว่า one-to-many นั่นแหละครับน้อง ๆ
ดังนั้นเห็นได้ชัดเลยว่า ฟังก์ชันผกผันตรีโกณมิติ (ในกรณีนี้คือ \(\arcsin\)) ว่ามันไม่เป็นฟังก์ชัน ดังนั้น เลยเป็นที่มาที่เราจะกำหนดเรนจ์ (ค่า Y) เพื่อให้ \(\arcsin\) เป็นฟังก์ชัน ดังรูปด้านล่างเลย
เราจะตัดเอาแค่ส่วนคำตอบ มุม \(-\dfrac{\pi}{2}\) ถึง \(\dfrac{\pi}{2}\) หากน้องสังเกตช่วงนี้ดี ๆ ตามภาพด้านบน จะเห็นว่า ไม่มีส่วนไหนที่เราลากเส้นตั้งฉากแกน X แล้วตัดกราฟเกิน 1 จุด
arcsin arccos arctan
สรุปง่าย ๆ คือ \(y=\arcsin{x}\) โดยเรนจ์คือ \(\left[-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right]\)
ต่อมาเรามาดู \(\arccos\) จะคล้าย ๆ กัน หากน้องวาดกราฟเราจะได้ดังรูปด้านล้างซึ่งสังเกตได้ว่าหากเรากำหนดช่วงเรนจ์ที่สนใจแค่ \(\left[0, \pi\right]\)
ส่วน \(\arctan\) ก็คล้าย ๆ กัน หากวาดกราฟพลิกแกนแล้วน้องก็จะได้ประมาณนี้ ซึ่งเรนจ์เราก็ตัดมาแค่ช่วง \(\left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right)\) บางคนอาจสงสัยว่า ทำไมเป็น ช่วงเปิด เครื่องหมาย '(' และ ')' มันหมายความว่า \(\arctan\) ไม่มีทางให้ค่ามุม \(\dfrac{\pi}{2}\) หรือ \(-\dfrac{\pi}{2}\) เพราะว่า? ใช่แล้วครับ เพราะ \(\tan\dfrac{\pi}{2}\) กับ \(\tan\left(-\dfrac{\pi}{2}\right)\) หาค่าไม่ได้นั่นเอง ดังนั้น มุมสองตัวนี้เลยไม่มีทางเป็นไปได้
พี่อาจจะไม่ได้ลงลึกเรื่องกราฟมากนะครับ เนื่องจาก รายละเอียดพวกกราฟไม่ได้เป็นจุดสำคัญขนาดที่ต้องเอาไปใช้สอบ แต่พี่แปะไว้ให้น้องได้รู้ว่า เรนจ์ของฟังก์ชัน arc- เนี่ยมันมีที่มายังไงบ้าง) ดังนั้นสิ่งที่น้องต้องจำให้ได้มีแค่เรนจ์ของ \(\arcsin, \arccos, \arctan\) แค่นั้นเองในการทำโจทย์ เดี๋ยวมีตัวอย่างโจทย์เพื่อความเข้าใจต่อด้านล่าง
\(y=\arcsin{x}\) โดยเรนจ์คือ \(\left[-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right]\)
\(y=\arccos{x}\) โดยเรนจ์คือ \(\left[0, \pi\right]\)
\(y=\arctan{x}\) โดยเรนจ์คือ \(\left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right)\)
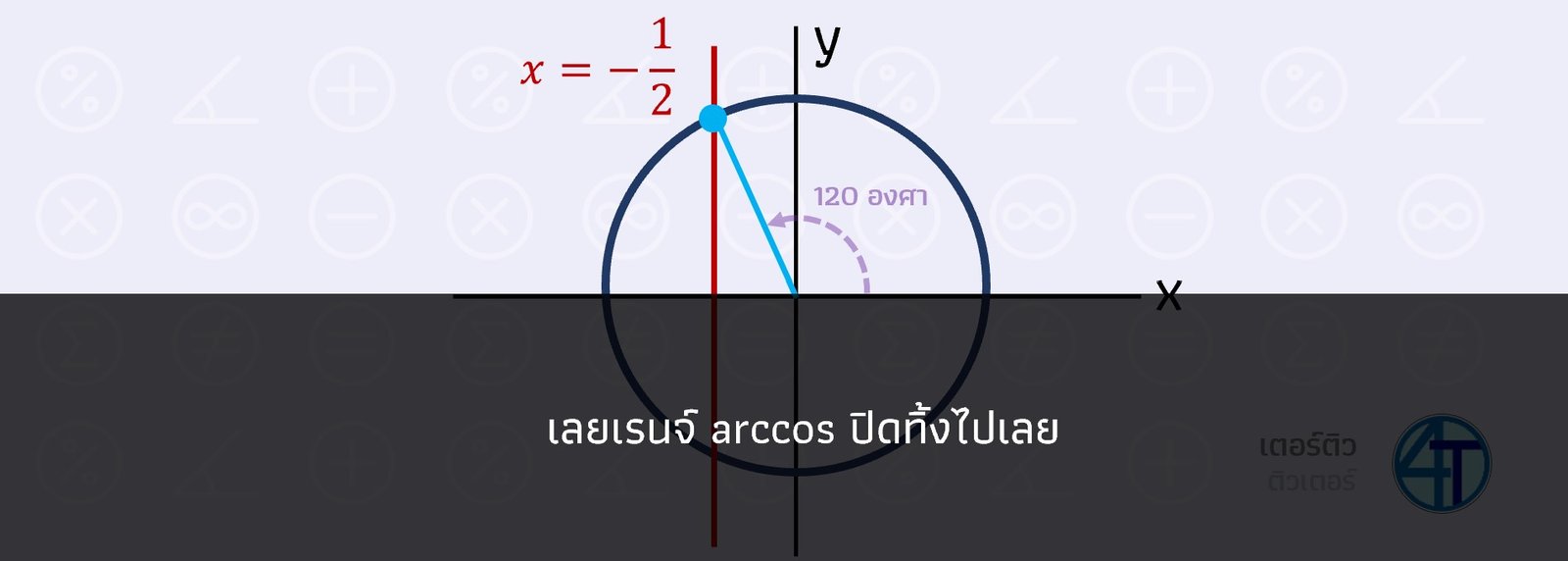
ตัวอย่างการค่าหา arc- function
จงหาค่าของ \(\arcsin\left(-\dfrac{1}{2}\right)\)
ในข้อนี้ถ้าน้องตอบได้เลย ถือว่าน้องเข้าใจคอนเซปต์ไปแล้ว ซึ่งยินดีด้วยครับ เพราะเรื่อง arc- เป็นเรื่องที่หลาย ๆ คน มักสับสนว่า มันต้องตอบมุมไหนกันแน่เนี่ยพี่
เรารู้ว่าโจทย์ถาม \(\sin\) มุมอะไรที่ให้ค่าเป็น \(-\dfrac{1}{2}\) ดังนั้นน้องก็ลองนึกภาพวงกลม 1 หน่วยคร่าว ๆ เรารู้ว่า cos x sin y ดังนั้นค่า \(\sin\) คือ \(y=-\dfrac{1}{2}\) เราก็ลากแกนเส้นตรง \(y=-\dfrac{1}{2}\) ได้เลย ได้ดังรูปด้านล่าง
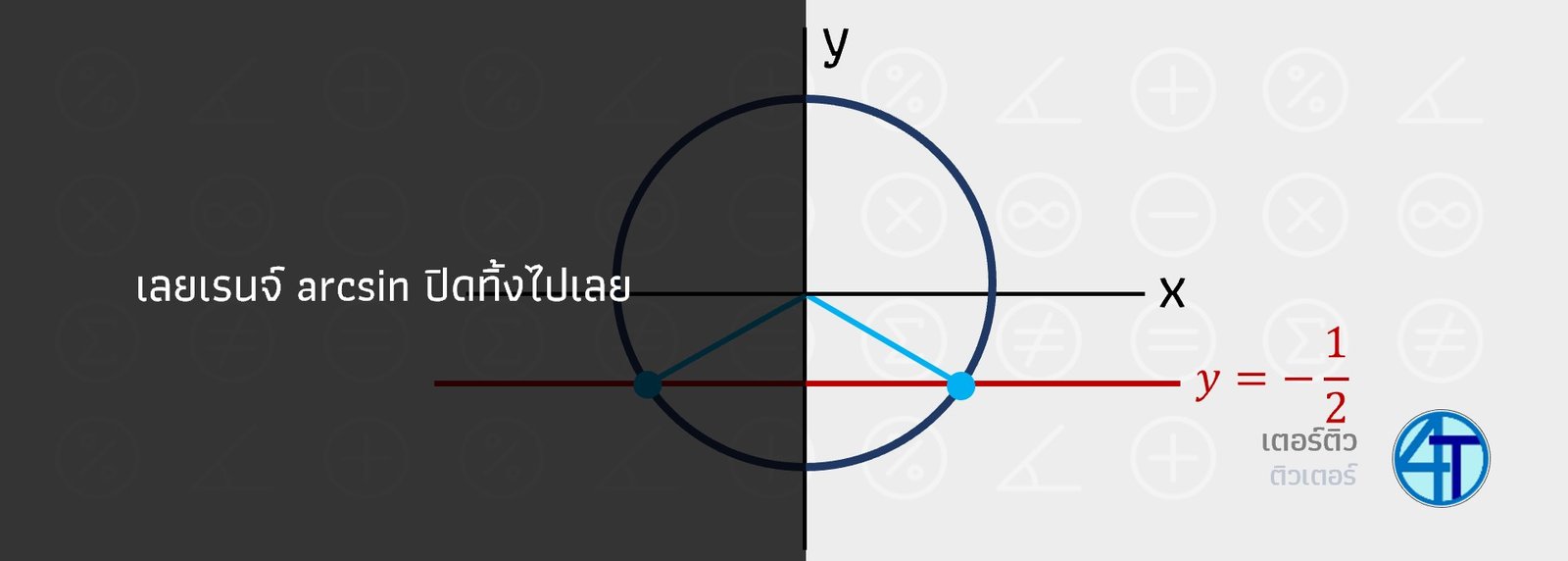
น้องจะสังเกตว่าตรง \(y=-\dfrac{1}{2}\) ตัดวงกลม 2 จุดด้วยกันซึ่งนั่นแปลว่า สองจุดนี้แหละที่ค่า \(\sin\) เป็น \(-\dfrac{1}{2}\) แต่ฝั่งซ้ายที่พี่ผิดไปเนื่องจากมันเลย เรนจ์ของ \(\arcsin\) ไปแล้ว
วิธีทำแบบเข้าใจหลักการง่าย ๆ คือ น้องต้องตอบจุดฟ้าฝั่งขวา (อันที่ไม่ได้โดนปิด) บางคนถามพี่ต่อว่า มุมนั้นคือ \(330^\circ\) ปะครับ ถูกครับน้อง แต่... เราตอบ \(330^\circ\) ไม่ได้ เพราะมันเลยช่วงเรนจ์ \(\arcsin\) ไปแล้ว เนื่องจากเรนจ์ \(\arcsin\) มีค่าแค่ \([-90^\circ, 90^\circ]\) แค่นั้น ดังนั้นน้องต้องกวาดมุมลงมาทางลบ ครับ จะได้ว่ามุมนั้นคือ \(-30^\circ\)
เคล็ดลับหาค่า arc-
ทริคที่แนะนำคือตรงที่ปิดไป เราจะไม่กวาดมุมผ่าน ให้น้องนึกถึงกำแพง เราไม่สามารถกวาดมุมผ่านมันได้ ซึ่งหากน้องต้องการ ตอบว่า \(330^\circ\) น้องต้องกวาดผ่านกำแพง ดังนั้นไม่ได้เนอะ
ดังนั้นข้อนี้จึงตอบ \(\arcsin\left(-\dfrac{1}{2}\right)=-\dfrac{\pi}{6}\)
ตัวอย่างเพิ่มเติม และหลักการหาค่า arc- ของมุมติดลบ โดยไม่ต้องนึกถึงวงกลมหนึ่งหน่วยตลอดเวลา น้อง ๆ สามารถดูเพิ่มเติมได้ที่คลิปสอนด้านบนนะครับ
รวมร่าง arc กับ ไม่-arc (ฟังก์ชันเดียวกัน)
ฟังก์ชันเดียวกัน เช่น \(\sin(\arcsin x)\) หรือ \(\cos(\arccos x)\)
แบบที่ 1 (arc- ข้างใน) เช่น sin(arcsin) ถ้าสองฟังก์ชันมาประกบกันแบบนี้ ยกตัวอย่าง \(sin(\arcsin(\dfrac{1}{2}))\) เนื่องจาก \(\sin\) กับ \(\arcsin\) เป็นฟังก์ชันผกผันซึ่งกันและกัน ดังนั้น น้องสามารถตัดมันทิ้งได้เลย \(\enclose{horizontalstrike}{sin(arcsin}(\dfrac{1}{2}))\) ก็เลยตอบ \(\dfrac{1}{2}\)
แบบที่ 2 (arc- ข้างนอก) ** ต้องระวัง ถามว่าตัดเลยได้มั้ย ตอบได้ว่าหลักการตัดเหมือนกัน แต่น้องต้องระวังนิดนึง ดูตัวอย่างเพื่อให้เห็นภาพมากขึ้น เช่นพี่มี \(\arcsin(\sin(\dfrac{5\pi}{6}))\) ถ้าน้องตัดเลยแบบนี้ \(\enclose{horizontalstrike}{\arcsin(\sin}(\dfrac{5\pi}{6}))\) จะตอบ \(\dfrac{5\pi}{6}\) ซึ่งผิด เพราะว่า arcsin มีเรนจ์แค่ \([-90^\circ, 90^\circ]\) เอง จะคืนค่าเป็น \(\dfrac{5\pi}{6}\) หรือ \(150^\circ\) ไม่ได้
เพราะฉะนั้นแล้วเราต้องหาตัวแทนมุมที่ตอบได้ ที่มีค่าเท่ากับค่าจากมุม \(150^\circ\) หากเราสังเกตจากรูปด้านล่างแล้ว น้องจะพอมองออกว่า cos x sin y ดังนั้น sin คือค่า y ซึ่งมุมใน Q2 (จตุภาคที่ 2) สามารถสะท้อนมาตอบเป็นมุมใน Q1 ได้ ส่วน Q3 ก็ตอบของ Q4 ได้
ดังนั้นหากเรากลับมาดูที่โจทย์ตั้งต้น \(\arcsin(\sin(\dfrac{5\pi}{6}))\) เราก็ตัดปกติ \(\enclose{horizontalstrike}{\arcsin(\sin}(\dfrac{5\pi}{6}))\) แต่เราจะสะท้อนมุม \(\dfrac{5\pi}{6}\) ไปตอบ \(\dfrac{\pi}{6}\) แทนนั่นเอง
ดังนั้น \(\arcsin(\sin(\dfrac{5\pi}{6}))=\dfrac{\pi}{6}\)
แล้ว \(\arccos\) เหมือนกันหรือเปล่า? ก็มีความคล้ายคลึงครับน้อง ๆ แต่ \(\arccos\) เนี่ย มันมีเรนจ์อยู่ช่วง \([0^\circ, 180^\circ]\) ซึ่ง cos คือ x ดังนั้น หากคำตอบเราอยู่ใน Q3 หรือ Q4 เราก็แค่ตบมันกลับมาตอบที่ Q2 หรือ Q1 ตามภาพด้านล่างง่าย ๆ แบบนี้เลย เพราะค่า x มันมีค่าแทนกันนั่นเอง
ส่วน \(\arctan\) หากน้อง ๆ จำได้มันมีเรนจ์เหมือน \(\arcsin\) ยกเว้นช่วงมุม \(\pm\dfrac{\pi}{2}\) ที่ไม่ใช่ ดังนั้น น้องก็ทำแบบเดิมปิดช่วงที่ไม่ได้เป็นกำแพงกั้นไว้ หากมุมที่น้องได้อยู่ในช่วงที่ตอบไม่ได้ เราก็ต้องเลื่อนมันไป ประเด็นคือเลื่อนไปตอบตรงไหน
ทำไม arctan ถึงทำเหมือน arcsin กับ arccos ไม่ได้
การที่ arcsin สามารถเลื่อนขวาไปตอบได้นั้น เพราะว่า sin คือค่า y และการเลื่อนขวา ค่า y ไม่ได้เปลี่ยน ส่วน arccos สามารถเคลื่อนบนไปตอบได้นั้น เพราะว่า cos คือค่า x และการเลื่อนบนค่า x ก็ไม่ได้เปลี่ยนอีกเช่นกัน ส่วน arctan ค่า tan คือ \(\dfrac{sin}{cos}\) ดังนั้น มันคือ \(\dfrac{y}{x}\) เลื่อนไปยังไงให้ค่าไม่เปลี่ยนดีหล่ะ?
(หากอ่านแล้วยังงง สามารถดูที่คลิปประกอบได้เพิ่มเติมนะครับ) หากน้องพิจารณารูปด้านล่าง น้องจะสังเกตว่าจุดตรง Q2 หากเราเลื่อนไปตอบตรง Q1 ค่า x มันจะกลับเครื่องหมายแค่ตัวเดียว \(y\) ไม่กลับ ดังนั้น มันจะเปลี่ยนเครื่องหมายแค่ตัวล่าง ใน \(\dfrac{y}{x}\) ของ \(tan\) ทำให้ค่าผิด
แต่หากสังเกตดี ๆ ถ้าเรากลับเครื่องหมาย ทั้งสองตัว ผลลัพธ์ก็จะเป็นตัวเดิม ตัวอย่างเช่น \(\dfrac{5}{\textcolor{blue}{-}8}=\dfrac{\textcolor{blue}{-}5}{8}\) หรือ \(\dfrac{\textcolor{blue}{-}2}{\textcolor{blue}{-}9}=\dfrac{2}{9}\) ดังนั้น หากการกลับสองเครื่องหมายจะทำให้ค่าไม่เปลี่ยน เราจึงต้องเลื่อนทแยง จาก Q2 ตอบ Q4 และก็จาก Q3 ตอบ Q1
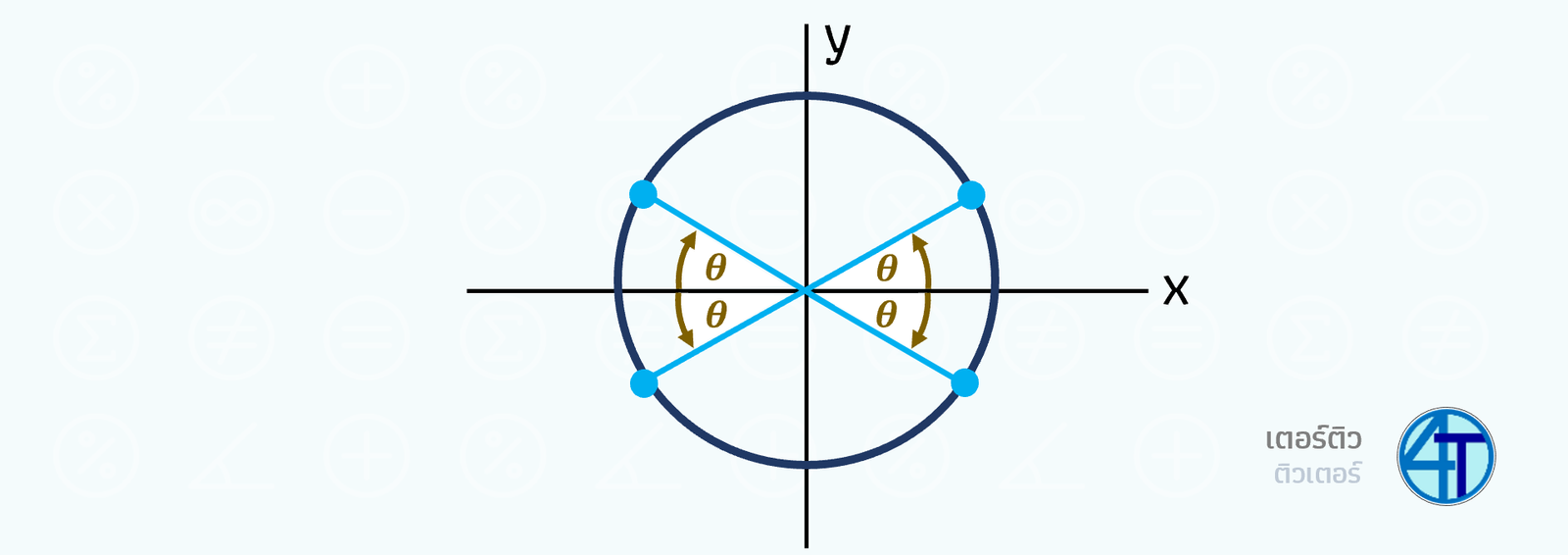
หากน้อง ๆ สงสัยว่าตอนเลื่อนไปหามุมที่ตอบจะรู้ได้ไงว่ามุมไหน ลองมองมุมแกน X เพื่อนบ้าน กันดูนะครับ มันจะสมมาตรกันทั้งหมดทั้ง 4 จตุภาค
รวมร่าง arc กับ ไม่-arc (ฟังก์ชันคนละตัว)
ฟังก์ชันไม่เหมือนกัน เช่น \(\sin(\arccos x)\) หรือ \(\tan(\arcsin x)\)
ถ้าเป็นแบบนี้ก็เหมือนเป็นคนละหมู่บ้าน เราก็ต้องค่อย ๆ คิดตรง ๆ ไปเลย (มันจะมีโจทย์ที่คิดตรง ๆ ไม่ได้ ซึ่งจะกล่าวต่อไปหลังจากส่วนนี้) สมมติโจทย์ถามว่า \(\tan(\arcsin(\dfrac{\sqrt{3}}{2}))\) โจทย์แบบนี้ มีวิธีทำสองวิธี วิธีแรกคือค่อย ๆ คิด หากเป็นมุมที่เรารู้ค่า ถ้าน้องสังเกตต้องทำจากในวงเล็บก่อน นั่นก็คือ \(\arcsin(\dfrac{\sqrt{3}}{2})\) ก็คือโจทย์ถามว่า sin มุมอะไรนะที่มีค่า \(\dfrac{\sqrt{3}}{2}\) ซึ่งอันนี้เรารู้ เราจึงตอบได้ว่าคือ \(60^\circ\)
ดังนั้น \(\tan(\arcsin(\dfrac{\sqrt{3}}{2}))=\tan(60^\circ)\) ซึ่งก็จะตอบว่า \(\sqrt{3}\) นั่นเอง
แล้วหากเราเจออันที่หาค่าไม่ได้หล่ะพี่ เช่น \(\sin(\arctan(-\dfrac{4}{5}))\) เนื่องจากเราไม่สามารถหา \(\arctan(-\dfrac{4}{5})\) ได้ เพราะไม่มีมุมมาตรฐานที่เราเรียนที่ให้ค่า \(tan\) เป็น \(\dfrac{4}{5}\) ดังนั้น ต้องใช้ตัวช่วยครับ
ตัวช่วยเราก็คือ สามเหลี่ยมมุมฉาก เพื่อนแสนดีของเรานี่เอง
หลักการก็คือเราจะแทน \(arc-\) เป็นมุมและวาดสามเหลี่ยม
จากโจทย์ \(\sin(\arctan(-\dfrac{4}{5}))\) เราก็คิดจากข้างในเช่นเคย \(\arctan(-\dfrac{4}{5})\) ก็เหมือนการถามน้องว่า \(\tan\) มุมอะไร มีค่า \(-\dfrac{4}{5}\) ซึ่งเราก็สามารถสมมติเป็นมุม \(A\) และกัน
เราก็จะบอกว่า \(\tan(A)=-\dfrac{4}{5}\) เนื่องจากเครื่องหมายลบ ไม่สามารถใช้ได้กับสามเหลี่ยม (ด้านสามเหลี่ยมเป็นบวกเสมอ) ให้น้องทดเครื่องหมายไว้ในใจก่อน
เราจะวาดสามเหลี่ยมได้ตามภาพด้านบน ซึ่งน้องก็ใช้พีทาโกรัสในการหาด้านที่เหลือได้
เนื่องจากเราแทนว่าเป็นมุม \(A\) ดังนั้น \(\sin(\arctan(-\dfrac{4}{5}))=\sin(A)\) (เครื่องหมายคิดหลังสุด) ตามสามเหลี่ยมมุมฉากที่เราวาด เราก็ได้ว่า sin คือ ข้าม/ฉาก ดังนั้นเลยได้ \(\sin(A)=\dfrac{4}{\sqrt{41}}\)
ดังนั้น ข้อนี้ก็เหมือนตอบว่า คือ \(\dfrac{4}{\sqrt{41}}\) แต่ อย่าลืมเครื่องหมายที่ทดไว้ การที่ \(\tan\) จะเป็น \(-\dfrac{4}{5}\) ก็ต้องอยู่ในจตุภาคที่ 4 (เรนจ์ \(\arctan\) คือ Q1 กับ Q4) ดังนั้น Q4 ค่า sin ต้องเป็น ลบ
คำตอบข้อนี้จึงตอบว่า \(\sin(\arctan(-\dfrac{4}{5}))=-\dfrac{4}{\sqrt{41}}\)
เรื่องนี้เป็นเรื่องที่ไม่ซับซ้อน แต่พี่แนะนำให้น้องดูวิดีโออีกทีบนหน้านี้ เนื่องจากพี่จะเพิ่มเติมโจทย์ตัวอย่างให้ และก็การอธิบาย ด้วยภาพและเสียงน้องน่าจะเข้าใจได้ง่ายมากขึ้น
หากบทความพี่เป็นประโยชน์ ฝากแชร์ต่อให้เพื่อนๆ ด้วยนะครับ :')