เลือกอ่านตามหัวข้อ?
ทบทวนสมบัติเลขยกกำลัง ม.1
หากน้อง ๆ จำได้ เลขยกกำลังเราได้เกริ่นกันไปในระดับชั้น ม.1 ซึ่งน้องได้เจอสมบัติของเลขยกกำลังบางตัวกันมาแล้ว ทั้ง 5 ตัวด้านล่าง ไม่ว่าจะเป็นสมบัติการคูณเลขยกกำลัง สมบัติการหารเลขยกกำลัง การยกกำลังด้วย \(0\) หรือ \(1\) และตัวสุดท้ายคือการยกกำลังด้วยเลขติดลบนั่นเอง

ใบบทนี้ระดับชั้น ม.2 เราจะมาเรียนเพิ่มอีกบาง สมบัติเลขยกกำลัง ที่สำคัญ เพื่อให้เราทำโจทย์ได้อย่างครอบคลุม ซึ่งจริง ๆ มันก็คือเรื่องต่อกันเลยครับน้อง ๆ ถ้าใครยังไม่แม่นสมบัติเลขยกกำลังทั้ง 5 ตัวด้านบน น้อง ๆ สามารถกลับไปทวนก่อนได้ที่หัวข้อ เลขยกกำลัง ม.1 ได้เลยนะ
1. สมบัติเลขยกกำลัง \((a^m)^n=a^{mn}\)

เราจะมาค่อย ๆ ดูทีละตัวกัน สมบัติเลขยกกำลัง ตัวแรกคือ หากเรามีเลขยกกำลังแล้วยกกำลังอีกที เราสามารถนำเลขยกกำลังมาคูณกันได้เลย
\((a^m)^n=a^{mn}\)
ตัวอย่างการใช้เช่น \((4^2)^3\) เราสามารถดึง \(3\) เข้ามาคูณกับกำลัง \(2\) ได้เลยเป็น \(4^{2\times 3}=4^{6}\) ทีนี้เราจะมาดูกันว่าทำไมถึง นำเลขยกกำลังมาคูณกัน ได้เลย ให้น้อง ๆ นึกถึงคอนเซปต์เลขยกกำลังไว้เสมอครับ เลขยกกำลังคือการคูณกันซ้ำ ๆ ตัวเดิม

จากภาพ ถ้าจะมองให้ง่ายคือเราจะทำในวงเล็บก่อน \(4^2\) เรารู้อยู่แล้วว่า \(4^2=4\times4\) พี่อยากให้น้อง ๆ ปิด \(4\times 4\) ด้วยกล่องและมองมันเป็นก้อน ๆ เดียวนะ ที่เรากำลังจะนำมันไป ยกกำลัง 3 เราก็จะได้ว่า นำกล่องคูณกับตัวมันเองไป 3 ตัว
\(\boxed{4\times 4}^3=\boxed{4\times4}\times\boxed{4\times4}\times\boxed{4\times4}\)
เราจะสังเกตว่า ทั้งหมดก็เป็นเครื่องหมายคูณ ดังนั้นเราก็สามารถรวมมันได้ แต่มันจะแตกต่างจากสมบัติเลขยกกำลัง \(a^m\cdot a^n=a^{m+n}\) ตรงที่ว่า แต่ละก้อนสี่เหลี่ยมก็มี \(4\) คูณกัน 2 ตัว และเราคูณมันทั้งหมด 3 ก้อน ดังนั้น จะมี \(4\) ทั้งหมด
(3 ก้อน) \(\times\) (ก้อนละ 2 ตัว) \(=3\times2=6\) ตัว
นี่แหละครับเป็นที่มาว่าทำไมเราถึงจับ เลขยกกำลัง มาคูณกันได้เลย ได้เป็นสมบัติเลขยกกำลัง อันนี้ \((a^m)^n=a^{mn}\) ซึ่งมันก็สามารถสลับที่ได้ด้วย เพราะการคูณมีสมบัติการสลับที่ เราเลยได้ว่า \((a^m)^n=a^{mn}\) \(=a^{\color{blue}{nm}}=(a^n)^m\)
\(\left(a^m\right)^n\) กับ \(a^{m^n}\) ไม่เหมือนกัน !
จุดนี้ต้องระวังด้วยนะครับน้อง ๆ เพราะว่าการที่เราใส่วงเล็บกับไม่ใส่วงเล็บนั้นช่างแตกต่าง แบบแรก \(\left(a^m\right)^n\) ก็คือแบบในสมบัติเลขยกกำลังด้านบน แต่แบบหลัง เราจะต้องนำเลขยกกำลังมายกกำลังกันก่อน และค่อยกลับมาให้ฐาน อารมณ์เหมือนทำจากบนลงล่างนั่นเอง
ตัวอย่างเช่น \(4^{2^3}\) เราจะคิดจากด้านบนสุด คือ \(4^{\color{blue}{2^3}}\) ซึ่ง \(2^3\) ได้ \(8\) ดังนั้น \(4^{2^3}=4^8\) ซึ่งมีค่าไม่เท่ากับ \((4^2)^3=4^{2\times3}=4^6\)
และถ้าน้องเจอยกกำลังซ้อนกันแบบหลาย ๆ ชั้นหล่ะ เช่น \(3^{1^{3^2}}\) เราก็จะเริ่มทำจากด้านบนนั่นเอง \(3^{1^{\color{blue}{3^2}}}=3^{1^{\color{blue}{9}}}=3^{\color{red}{1^9}}=3^{\color{red}{1}}=3\) ซึ่งจะแตกต่างกับตัวอย่างโจทย์ด้านล่าง ลองฝึกทำกันดูนะ
ทีนี้หากพี่ถามน้อง ๆ ว่า \(\left(a^m\right)^n\ne a^{m^n}\) เสมอ ใช่หรือไม่ เนื่องจากน้อง ๆ รู้แล้วว่ามันคิดไม่เหมือนกัน ดังนั้นค่ามันก็ไม่เหมือนกันถูกต้องแล้วครับ แต่ในบางกรณี มันก็เท่ากันได้นะ เช่น \(\left(2^2\right)^2\) กับ \(2^{2^2}\) ทั้งสองมีค่าเป็น \(2^4\) ทั้งคู่ ดังนั้น การที่บอกว่า \(\left(a^m\right)^n\ne a^{m^n}\) เสมอ ไม่ถูกต้อง
2. สมบัติเลขยกกำลัง \((ab)^n=a^nb^n\)
ถ้าน้อง ๆ มีเลขยกกำลังที่อยู่บนตัวอะไรกำลังคูณกัน เราสามารถกระจายยกกำลังให้แต่ละตัวได้เลย พี่อยากให้น้องมองภาพด้านล่าง เพียงแค่เราจับกลุ่มแบบใหม่ เราจะเห็นสมบัติเลขยกกำลังตัวนี้ชัดขึ้นเลยครับ
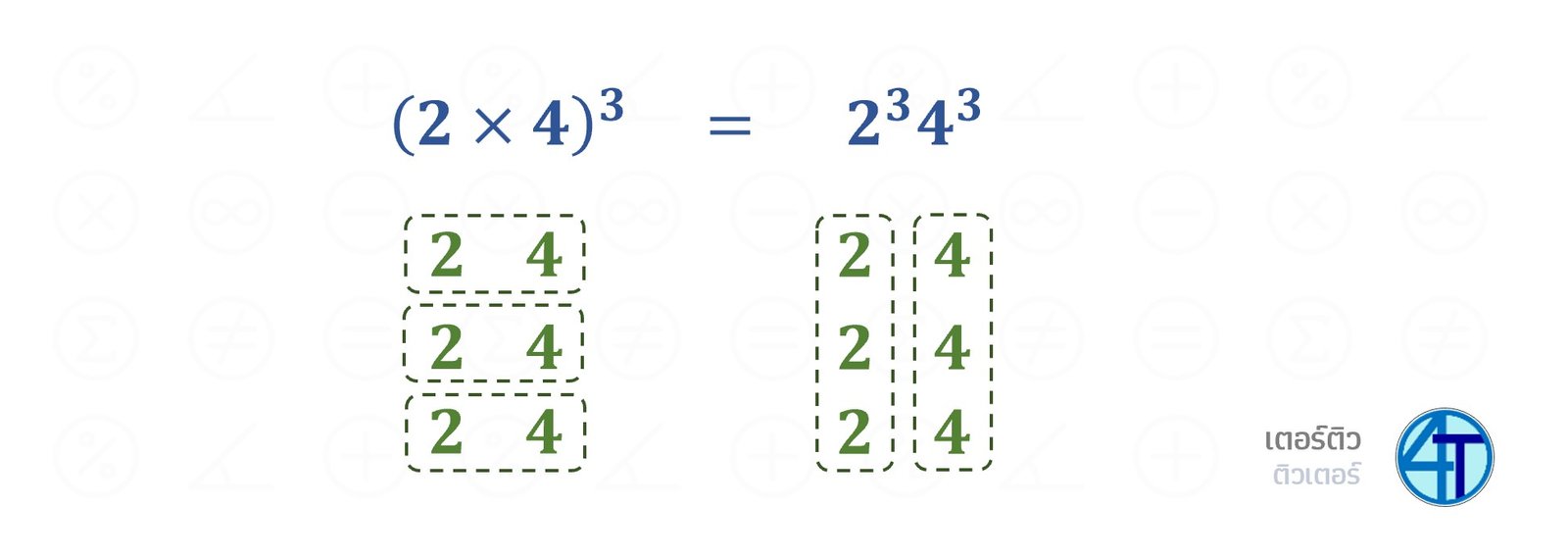
ด้านซ้ายพี่มี \((2\cdot4)^3\) ซึ่งหากเราจับกลุ่มแนวนอน น้อง ๆ จะได้ ก้อน \(\boxed{2\cdot4}\) คูณกันสามก้อน นั่นก็คือ \(\boxed{2\cdot4}^3\) แต่หากเราจับกลุ่มและมองแบบใหม่ แบบด้านขวามือ โดยการจับเลขเดียวกันคูณกันก่อน เราก็จะได้แยกเป็นแต่ละตัวยกกำลัง 3 ได้เป็น 2 พจน์ คือ \(2^3\) คูณกับ \(4^3\) ดังนั้น สมบัติเลขยกกำลัง ที่เราได้ก็จะเป็น
\((ab)^n=a^nb^n\)
ไม่เพียงแค่น้อง ๆ มีเลขสองตัวคูณกัน \(a\) กับ \(b\) แล้วยกกำลังเท่านั้นนะครับ แต่หากน้อง ๆ มีเลขหลายตัวคูณกันก็สามารถกระจายเลขยกกำลังเข้าไปได้เลย ถ้าทุกตัวคูณกันหมด เช่น \((abc)^n=a^nb^nc^n\) และ \((abcd)^n=a^nb^nc^nd^n\)
3. สมบัติเลขยกกำลัง \(\left(\dfrac{a}{b}\right)^n=\dfrac{a^n}{b^n}\)
ข้อนี้มองคล้าย ๆ ข้อที่แล้วได้เลยครับผม การหารกันก็เหมือนการคูณนั่นแหละครับน้อง ๆ เรากระจายเลขยกกำลังไปให้ทั้งเศษและส่วนได้เลย

จากภาพด้านบน น้อง ๆ จะเห็นได้ง่ายเลยครับว่าสมบัติข้อ 2 กับข้อ 3 ที่เราเรียนกัน มันมาจากวิธีจากจับกลุ่มเท่านั้นเอง ว่าน้อง ๆ จะทำตัวเลขตรงไหนก่อนกัน
\(\left(\dfrac{a}{b}\right)^n=\dfrac{a^n}{b^n}\)
และถ้ามันมีทั้งคูณและหารหล่ะ ?
สมมติเรามี \(\left(\dfrac{ab}{cde}\right)^n\) ก็ไม่ยากครับน้อง ๆ เราสามารถนำสองสมบัติมารวมกันและกระจาย ยกกำลัง \(n\) ให้ทุกตัวได้เลย จะได้เป็น \(\dfrac{a^nb^n}{c^nd^ne^n}\)
อย่างโจทย์ข้อบน หากน้อง ๆ คิดได้แล้วดูเฉลยกันแล้ว ลองย้อนกลับไปดูกันหน่อยครับว่า เราได้คำตอบของโจทย์นี้ใช้เวลาคิดนานประมาณไหน สำหรับพี่เวลาพี่แปลงเรื่องเลขยกกำลังให้เป็นรูปแบบอย่างง่าย พี่จะมีทริคว่า ให้ทำฐานแต่ละตัวแยกกัน เพราะว่าอะไรครับ เพราะว่าสมบัติเลขยกกำลังแทบจะทุกตัว ต้องมีฐานที่เหมือนกันนั่นเอง
\(\dfrac{10(a^2b^3)^2}{5a^4b^{-2}}\) ข้อนี้ พี่จะคิดแยกสามส่วน ส่วนแรกคือ สัมประสิทธิ์ตัวเลข ส่วนที่สองคือ \(a\) และส่วนสุดท้ายคือ \(b\)
สำหรับส่วนสัมประสิทธิ์ \(\dfrac{{\color{blue}{10}}(a^2b^3)^2}{{\color{blue}{5}}a^4b^{-2}}\) ใช่แล้ว เรามีแค่ \(\dfrac{10}{5}=2\)
สำหรับส่วนฐานที่เป็น \(a\) ส่วนเศษเราต้องกระจายเลขยกกำลังเข้ามาคูณ และตัวส่วนก็นำไปลบออก จะได้เป็น \(a^{2\times2-4}=a^0=1\)
สำหรับฐานที่เป็น \(b\) ก็จะได้เป็น \(b^{3\times2-(-2)}=b^8\)
จับทุกอย่างมารวมกันคูณกันได้ \(2b^8\) เป็นคำตอบของเรา
เลขยกกําลังเศษส่วน (ราก)
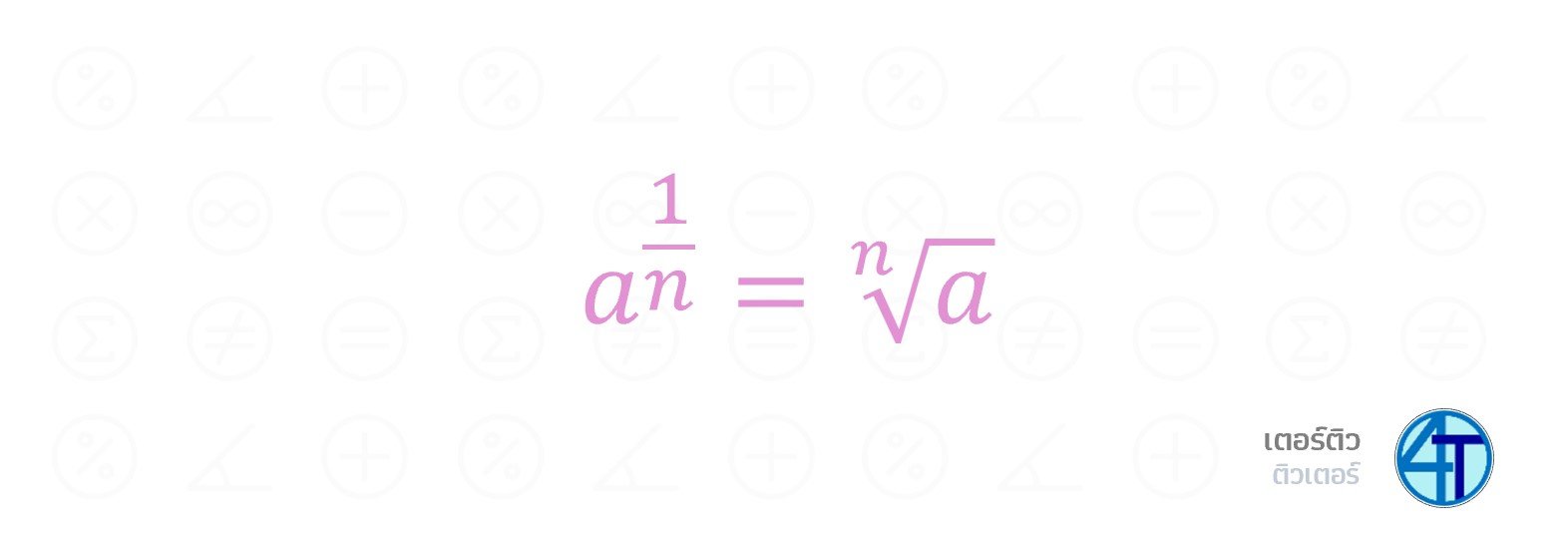
เนื่องจากเราได้เรียนเรื่อง รากที่สอง รากที่สาม และ รากที่ \(n\) กันไปแล้ว เรื่องเลขยกกำลังนี้ก็มีความเกี่ยวเนื่องกับรากอยู่เหมือนกันครับ โดยเราจะมีวิธีการเขียนรากในรูปแบบของการยกกำลัง โดยรากที่ \(n\) เราจะเขียนเป็นยกกำลัง \(\dfrac{1}{n}\) ใช่แล้วครับน้อง ๆ เลขยกกำลังเศษส่วน
\(\sqrt[n]{a}=a^{\frac{1}{n}}\)
ตัวอย่างเช่น \(5^{\frac{1}{2}}=\sqrt{5}\) การที่เรายกกำลังด้วย \(\dfrac{1}{2}\) ก็คือการที่เราถามหา รากที่สอง หรือใส่เครื่องหมายกรณฑ์ที่สองเข้าไปนั่นเอง
ซึ่งการเขียนรากแบบเลขยกกำลังมันจะไปเกี่ยวเนื่องกับการแก้สมการที่มีเลขยกกำลังเศษส่วนติดอยู่นั่นเอง เช่น บางทีน้องอาจจะเจอโจทย์ที่ให้มาเป็นราก และถ้าเราแปลงเป็นเลขยกกำลังอาจจะแก้ได้ง่ายกว่าโดยการใช้สมบัติของเลขยกกำลัง
สมการเลขยกกำลัง

หากน้อง ๆ จำได้ เราได้เรียนเรื่องสมการเชิงเส้นตัวแปรเดียวกันไปแล้วในระดับชั้น ม.1 ซึ่งการแก้สมการนั้นก็คือ การกระทำตัวดำเนินการมทางคณิตศาสตร์ทั้งสองฝั่งเหมือน ๆ กัน เช่น
\(x-6{\color{red}{+6}}=3{\color{red}{+6}}\)
เราจะนำ \(6\) ไปบวกให้ทั้งสองฝั่งของสมการเพื่อให้ฝั่งซ้ายเหลือแต่ \(x\) และได้คำตอบเป็น
\(\require{cancel}\begin{aligned} x-\cancel{6}+\cancel{6}&=9\\ x&=9 \end{aligned}\)
1. ยกกำลังด้วยส่วนกลับ
ในเรื่องการแก้สมการที่ติดเลขยกกำลัง แบบนึงที่น้อง ๆ สามารถเจอได้ก็คือ เลขยกกำลังเศษส่วนครับ เช่น สมมติ \(4^{\frac{1}{x}}=2\) หากเราอยากกำจัดเศษส่วนในเลขยกกำลัง วิธีนึงที่สามารถทำได้ก็คือ การยกกำลังด้วยส่วนกลับของมันทั้งสองฝั่งของสมการ อย่าลืมนะครับว่าการทำอะไรในสมการนั้น เราต้องทำพร้อมกัน เหมือนกันทั้งสองฝั่ง
จากโจทย์ที่เรามี \(4^{\frac{1}{x}}=2\) พี่จะยกกำลังด้วยส่วนกลับของ \(\frac{1}{x}\) ซึ่งก็คือ \(x\) เราจะได้ว่า \(\left(4^\frac{1}{x}\right)\color{red}{^x}=2\color{red}{^x}\) สมบัติเลขยกกำลัง บอกว่า ถ้าเราเจอกำลังซ้อนกันแบบนี้ ให้เราคูณเลขยกกำลังได้เลย ดังนั้น \(4^{\frac{1}{x}\times x}=2^x\) ด้านซ้ายเศษส่วนจะตัดกันครับ จะเหลือแค่ \(4=2^x\) เราจึงตอบได้ว่า \(x=2\) เพราะ สองยกกำลังสองได้สี่ นั่นเอง
ตัวอย่าง ต่อมา หากกำหนดให้ \(7^a=2\) จงหาค่าของ \(8^{\frac{1}{a}}\)
ถ้าสังเกตดี ๆ \(7^a=2\) เจ็ดยกกำลังอะไรได้สอง มันไม่น่าหาเป็นจำนวนเต็ม ๆ หรือจำนวนง่าย ๆ ออกมาได้เลย ดังนั้นข้อนี้เราจะไม่แก้หาค่า \(a\) ออกมาตรง ๆ แต่จะใช้วิธี แปลงสิ่งที่โจทย์ให้มาเป็นสิ่งที่โจทย์ถาม* ติดดาวไว้ได้เลยครับน้อง ๆ ทริคการทำโจทย์อีกรูปแบบที่เจอบ่อยในข้อสอบก็คือการจัดรูป แต่ไม่ต้องหาค่าตัวแปรออกมาจริง ๆ นั่นเอง
โจทย์ถามหา \(8^{\frac{1}{a}}\) ยกกำลัง \(\frac{1}{a}\) แต่โจทย์ให้ยกกำลัง \(a\) เรามา ดังนั้น วิธีนึงที่ทำได้ก็คือนำสมการ \(7^a=2\) มายกกำลังด้วย \(\frac{1}{a}\) ทั้งสองข้าง
\(\require{cancel}\begin{aligned} \left(7^a\right)^\frac{1}{a}&=2^\frac{1}{a}\\ 7^{a\times \frac{1}{a}}&=2^\frac{1}{a}\\ 7&=2^\frac{1}{a} \end{aligned}\)
อ่าว แต่โจทย์ถาม \(8^\frac{1}{a}\) นิ ซึ่งเรารู้แค่ \(2^\frac{1}{a}=7\) หากน้อง ๆ สังเกตดี ๆ จะเห็นว่า \(8=2^3\) ดังนั้น เราสามารถทำฐานให้เท่ากับสิ่งที่เรามีได้ เผื่อจะได้ใช้สมบัติเลขยกกำลังมาช่วย
โจทย์ถามหา \(8^\frac{1}{a}=\left(2^3\right)^\frac{1}{a}=\left(2^\frac{1}{a}\right)^3\) ทีนี้เราก็ได้สิ่งที่เรามีแล้วครับ เรารู้ว่า \(2^\frac{1}{a}=7\) ดังนั้น \(\left(2^\frac{1}{a}\right)^3=7^3=7\times7\times7=343\)
2. ทำฐานให้เท่ากัน
ถ้าเรามีสมการและมีเลขยกกำลังอยู่ในสมการด้วย เราจะมีทริคการแก้โจทย์สองแบบด้วยกัน แบบแรกคือ การทำฐานให้เท่ากัน การทำฐานให้เท่ากัน สิ่งที่เราจะได้ก็คือ เราสามารถจับเลขยกกำลังมาเท่ากันได้เลย

สมมติว่าเรามีโจทย์ \(3^{x+2}=9^{2x-5}\) สิ่งที่เราเห็นก็คือ ฐานไม่เท่ากัน แต่ฐานนั้น สัมพันธ์กันในรูปแบบของเลขยกกำลัง แบบนี้เราจะพยายามแปลงฐานให้เท่ากัน เมื่อเรารู้ว่า \(9=3^2\) เราจะแปลงให้ฝั่งขวาอยู่ในรูปแบบของ ฐาน \(3\) ด้วยเช่นกัน
\(\require{cancel}\begin{aligned} 3^{x+2}&=\color{blue}{\left(3^2\right)}^{2x-5}\\ 3^{x+2}&=3^{2\times{(2x-5)}}\\ 3^{x+2}&=3^{4x-10} \end{aligned}\)
เมื่อเราแปลงโจทย์ให้ฐานเท่ากันแล้ว เราสามารถจับเลขยกกำลังมาเท่ากันได้เลย จะได้ว่า \(x+2=4x-10\) ซึ่งเราก็จะแก้สมการออกมาได้เป็น \(3x=12\rightarrow x=4\)
ทริคการตรวจคำตอบ
เวลาทำโจทย์ส่วนมากมีโอกาสที่เราจะคิดเลขผิดแน่นอนอยู่แล้วครับ ซึ่งหากการตรวจคำตอบไม่ได้ทำให้เราเสียเวลาเยอะ พี่อยากให้น้อง ๆ แทนค่าคำตอบกลับไปในสมการที่เรามีด้วยว่าถูกต้องหรือไม่ อย่างข้อบนเมื่อเรารู้ว่า \(x=4\) เราจะแทนในส่วนของเลขยกกำลัง \(x+2\) และ \(4x-10\) ปรากฎว่าทั้งสองมีค่า \(6\) ดังนั้น คำตอบจึงถูกต้องแล้ว
3. ทำเลขยกกำลังให้เท่ากัน
หากตัวฐานมันไม่มีความสัมพันธ์กันในเชิงเลขยกกำลังและเราไม่สามารถทำฐานให้เท่ากันได้ อีกวิธีคลาสสิกที่น้อง ๆ สามารถทำได้ก็คือการจัดรูปให้เลขยกกำลังเท่ากัน จากนั้นเราจะแก้สมการจับฐานเท่ากันได้เลย

สมมติว่าเรามี \((x+2)^{13}=6^{26}\)
เนื่องจากสิ่งที่เราต้องการ คือ \(x\) และ \(x\) ของเราก็เป็นตัวฐาน ดังนั้น เราอยากได้สมการที่สามารถจับฐานเท่ากันมาแก้สมการได้ ข้อนี้เราจึงอยากจะแปลงเลขยกกำลังให้เท่ากันเพื่อจะได้ตัดออกได้
เนื่องจากเลขยกกำลังฝั่งซ้ายคือ \(13\) แต่ฝั่งขวาเราเป็น \(26\) ดังนั้นเราจะแยกตัวประกอบของตัวมากกว่าให้มีติดเลขตัวน้อยกว่า เนื่องจากเรารู้ว่า \(26=13\times 2\)
\(\require{cancel}\begin{aligned} (x+2)^{13}&=6^{13\times 2}\\ (x+2)^{13}&=6^{2\times 13}\\ (x+2)^{13}&=(6^2)^{13}\\ \end{aligned}\)
เนื่องจากเรามีเลขยกกำลังที่เท่ากัน เราสามารถตัดเลขยกกำลังและจับฐานเท่ากันได้เลย จะได้ว่า
\(\)
\(\require{cancel}\begin{aligned} x+2&=6^2\\ x+2&=36\\ x&=34 \end{aligned}\)
4. เลขยกกำลังที่ผลเป็นหนึ่ง
สมการในอีกรูปแบบที่น้อง ๆ สามารถเจอได้ก็คือการใช้สมบัติของเลขยกกำลังที่เรารู้ว่า \(a^0=1\) และ \(1^a=1\)
\((a^0=1)\Rightarrow\) อะไรยกกำลัง \(0\) ได้ \(1\)
\((1^a=1)\Rightarrow\) \(1\) ยกกำลังอะไรก็จะได้ \(1\)
จะสังเกตว่าทั้งสองกรณีเราได้คำตอบเป็น \(1\) ทั้งคู่ ดังนั้น หากเรามี \((x+2)^{x-3}=1\) แบบนี้ เราไม่มีทางไปยกกำลังจริง ๆ ได้เลยครับ แต่เรารู้ว่าผลลัพธ์ฝั่งขวาเป็น \(1\) ซึ่ง แสดงว่า เรามีสองกรณี
แบบแรก คือ ฐานเป็น \(1\) เราจะได้ว่า \(x+2=1\) แก้ได้เป็น \(x=-1\)
แบบสอง คือ เลขยกกำลังเป็น \(0\) เราจะได้ว่า \(x-3=0\) แก้ได้เป็น \(x=3\)
ดังนั้น ข้อนี้ตอบว่า \(x=-1,3\)
หากบทความพี่เป็นประโยชน์ ฝากแชร์ต่อให้เพื่อนๆ ด้วยนะครับ :')
