ประพจน์ และ ตัวเชื่อมประพจน์ ม.4

ประพจน์ คือ อะไร

ในเรื่อง ตรรกศาสตร์ ที่เราจะเรียนกันใน ม.4 เป็นเรื่องที่เกี่ยวกับ ความสมเหตุสมผล หรือที่เราเรียกอีกอย่างว่า มีเหตุมีผล ดังนั้น ในเรื่อง ตรรกศาสตร์ เราจะสนใจ หาค่าความจริงของประโยคกัน ว่าประโยคเป็นจริงหรือเท็จ

แต่ประโยคที่น้องเจอในชีวิตประจำวันก็มีหลากหลายแบบ สมมติ "ช่วยไปปิดประตูให้หน่อย" ประโยคคำสั่งเชิงขอร้องที่กล่าวมา ถ้าถามว่า ค่าความจริงคืออะไร ก็จะดูงง ๆ ถูกมั้ยเอ่ย เพราะว่า มันไม่มีค่าความจริงนั่นเอง เพราะฉะนั้น ประโยคที่เราสนใจ ในเรื่อง ตรรกศาสตร์ เราจะ

สนใจแค่ประโยคที่มีค่าความจริง (สามารถเป็นจริงหรือเท็จก็ได้) ซึ่งเราเรียกประโยคเหล่านี้ว่า ประพจน์

สมมติเรามี ประโยค (ประพจน์) ว่า \(2\lt3\) ประโยคที่เป็นประพจน์นี้ ก็คือ มีค่าความจริง เป็น จริง เพราะ \(2\) ก็ย่อมน้อยกว่า \(3\) แต่ ประโยค (ไม่ใช่ประพจน์) ว่า \(x\gt7\) เป็นประโยคที่ค่าความจริงไม่ชัดเจน เช่น ถ้าเราแทน \(x\) เป็น \(3\) จะได้ \(3\gt7\) ดังนั้นเป็น เท็จ แต่หากเราแทน \(9\) เข้าไป จะได้ \(9\gt7\) ซึ่งเป็นจริง ดังนั้น ประโยคนี้เป็น ประโยคที่ไม่ใช่ประพจน์

ในเรื่อง ตรรกศาสตร์ ม.4 ที่น้องเจอเริ่มแรกก็ต้องแยกกันให้ออกก่อนว่า ประโยคไหนเป็นประพจน์และไม่เป็นประพจน์ ดังนั้น ไปลองทำแบบฝึกหัดข้างล่างเลย

จงหาว่าประโยคแต่ละอัน อันไหนไม่เป็นประพจน์ หรือ เป็นประพจน์ หากเป็นประพจน์ให้หาค่าความจริงด้วยว่า ประพจน์นั้นเป็นจริง หรือ เท็จ

เสริม หากเราถามว่า "มนุษย์ต่างดาวมีอยู่จริง" เป็นประโยคที่เป็นประพจน์หรือเปล่า น้อง ๆ อาจเกิดข้อสงสัยว่า มันหาค่าความจริงไม่ได้ เพราะเรายังไม่รู้ แต่มันก็มีค่าความจริงถูกมั้ย คือถ้าอนาคตอีกร้อยล้านปีเราหาเจอ ก็แปลว่า มีอยู่จริง ประพจน์ก็เป็นจริง หรือถ้าเราพิสูจน์ได้ว่าไม่มีจริงนะ ประพจน์ข้างต้นก็ไม่เป็นจริง ดังนั้น ให้น้องระวังไว้ด้วยว่า กรณีที่เรายังไม่รู้ค่าความจริง ก็สามารถเป็นประพจน์ได้เหมือนกัน

ตัวเชื่อมประพจน์ \(\vee\;\wedge\;\to\;\leftrightarrow\;\sim\)

ในเรื่อง ตรรกศาสตร์ ด้วยความที่เป็นบทในคณิตศาสตร์ เราก็จะไม่เขียนเวิ่นเว้อ แบบตัวอย่างด้านล่าง เรามักจะ แทนประพจน์ ด้วยตัวอักษร มักเริ่มที่ \(p\) ต่อไป \(q,r,s,t,\dots\) ตามจำนวนประพจน์ทั้งหมดที่ปรากฎในโจทย์

สังเกตว่า ประพจน์ข้างต้น มีประพจน์สองอันอยู่ด้วยกัน คือ (1) เมื่อวานฝนตก และ (2) เราสอบได้ที่หนึ่ง ทั้งสองอันสามารถหาค่าความจริงได้ โดยที่เรา เขียนแทนประพจน์ด้วยตัวอักษร

\(p\) แทนประพจน์ "เมื่อวานฝนตก"
\(q\) แทนประพจน์ "เราสอบได้ที่หนึ่ง"

ในพาร์ทนี้เราจะมาดูตัวเชื่อมประพจน์กันว่ามีอะไรบ้าง (อย่างตัวอย่างข้างบนก็คือ ตัวเชื่อม "และ" นั่นเอง)

และ \(\wedge\)

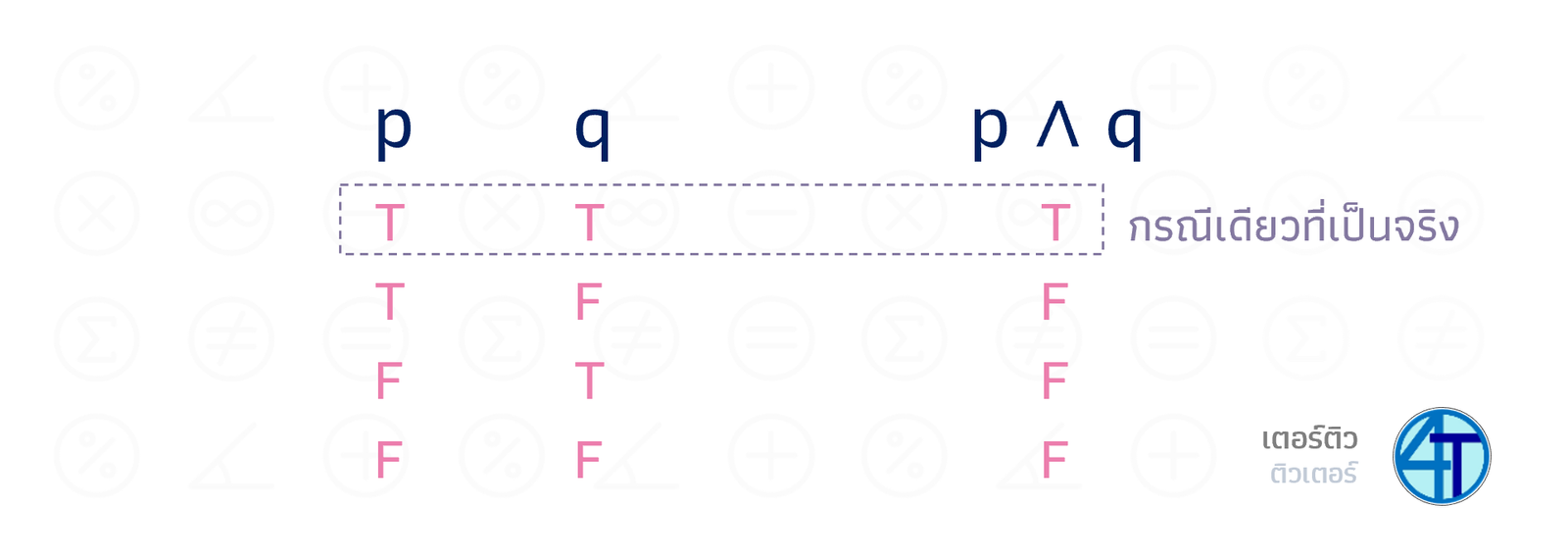
หากน้องสังเกตจากตัวอย่างข้างบน จะสังเกตว่า เรานำ \(p\) และ \(q\) มาเชื่อมกัน เกิดเป็นประพจน์ใหม่ นั่นก็คือ \(p\) และ \(q\) หรือเขียนเป็นสัญลักษณ์ว่า \(p\wedge q\) 

ตระหนักไว้เสมอเลยว่า มีประพจน์ ก็ต้องมีค่าความจริง ดังนั้น เราต้องหาค่าความจริง อันใหม่ ให้กับ \(p\wedge q\) โดยเราจะใช้ค่าความจริง ของ \(p\) และ \(q\) มาช่วยตัดสินใจว่า ค่าความจริงของ \(p \wedge q\) คืออะไร

สมมติง่าย ๆ ว่า เราต้องการซื้อของไปทำขนม ดังนั้น เราต้อง "ซื้อไข่และซื้อแป้ง" หมายความว่า ต้องซื้อทั้งสองอัน ถึงจะโอเค หากน้องซื้อมาแค่แป้ง หรือ ซื้อแค่ไข่ หรือไม่ซื้อเลย ประโยคที่ว่า "ซื้อไข่และซื้อแป้ง" ก็จะผิดทันที ดังนั้น การที่ประพจน์ใหม่ที่เราสร้างด้วย ตัวเชื่อม "และ" จะต้องจริงทุกตัว ถึงจะทำให้ประพจน์ใหม่เป็นจริง

หากเรามีสองประพจน์ \(p\) และ \(q\) เรานำมา "และ" กัน ได้ว่า \(p\wedge q\) เราจะได้ทั้งหมด \(4\) กรณี

(1) \(p\) เป็นจริง \(q\) เป็นจริง
(2) \(p\) เป็นจริง \(q\) เป็นเท็จ
(3) \(p\) เป็นเท็จ \(q\) เป็นจริง
(4) \(p\) เป็นเท็จ \(q\) เป็นเท็จ

เราจะนำมาใส่ตาราง (ตารางค่าความจริง ซึ่งจะกล่าวลึกขึ้นในบทถัดไป ตอนนี้เอามาช่วยให้น้อง ๆ เห็นภาพง่าย ๆ ก่อน) ได้ดังนี้

สังเกตกันได้เลยว่า กรณีเดียวที่ประพจน์ใหม่ \(p\wedge q\) จะเป็นจริงได้ ทั้ง \(p\) และ \(q\) ต้องเป็นจริงทั้งคู่

เราจะใช้ T แทน จริง (True) และ F แทน เท็จ (False)

เสริม หากมี 3 ประพจน์ มา "และ" กันทั้งหมดเลย \(p\wedge q\wedge r\) เราจะเขียนในตารางได้ \(8\) กรณี เช่น \(p\) จริง \(q\) เท็จ \(r\) จริง หรือ \(p\) เท็จ \(q\) เท็จ \(r\) จริง และ อื่น ๆ หากไล่ครบทุกกรณี น้องจะได้ \(8\) กรณี และเราจะเขียนตารางได้แบบด้านล่าง ซึ่ง กรณีเดียวที่เป็นจริงก็คือ ทั้งสามตัวเป็น จริง ทั้งหมด

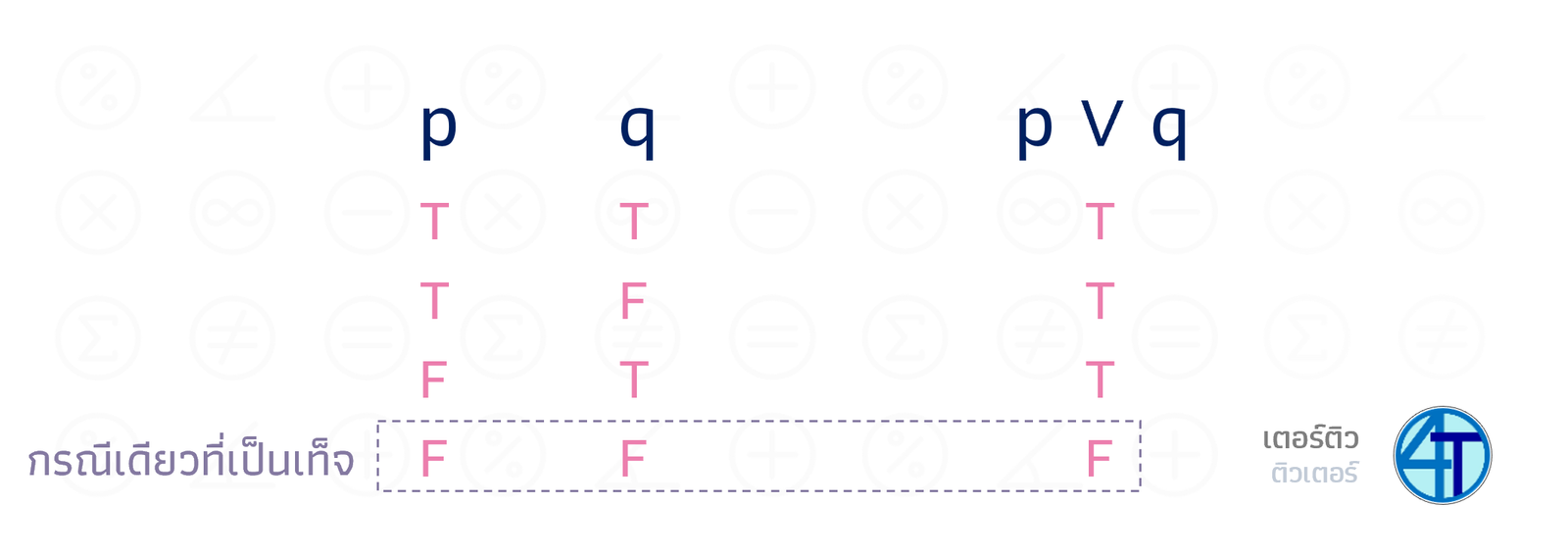
หรือ \(\vee\)

"หรือ" จะไอเดียกลับด้านกับ "และ" คือ สมมติ แม่ต้องการเขียนอะไรสักอย่าง แต่ที่บ้านไม่มีอะไรที่เขียนได้ แม่เลยบอกให้น้องออกไปตลาด ไปซื้อของให้หน่อย โดยประพจน์ของน้องคือ "ซื้อปากกาหรือซื้อดินสอ" สังเกตว่า ตามหลักความเข้าใจที่เราเข้าใจกันอยู่แล้วในหลักภาษาไทย เราจะรู้ว่า

(1) ซื้อปากกาอย่างเดียว
(2) ซื้อดินสออย่างเดียว
(3) ซื้อทั้งดินสอและปากกา

ทั้ง 3 กรณีที่กล่าวมาข้างบน แม่ก็โอเคหมดเพราะสามารถเขียนได้และ แต่มีอย่างนึงที่แม่ไม่ปลื้ม ก็คือ น้องไม่ได้ซื้ออะไรมาเลย หมายความว่า ประโยคที่เป็นประพจน์ที่บอกว่า "ซื้อปากกาหรือซื้อดินสอ" ผิด เพราะ ซื้อปากกา เป็น เท็จ และ ซื้อดินสอ ก็เป็น เท็จ นั่นเอง (เท็จทั้งคู่ = แม่ไม่โอเค = ประพจน์เป็นเท็จ)

ถ้า ... แล้ว \(\to\)

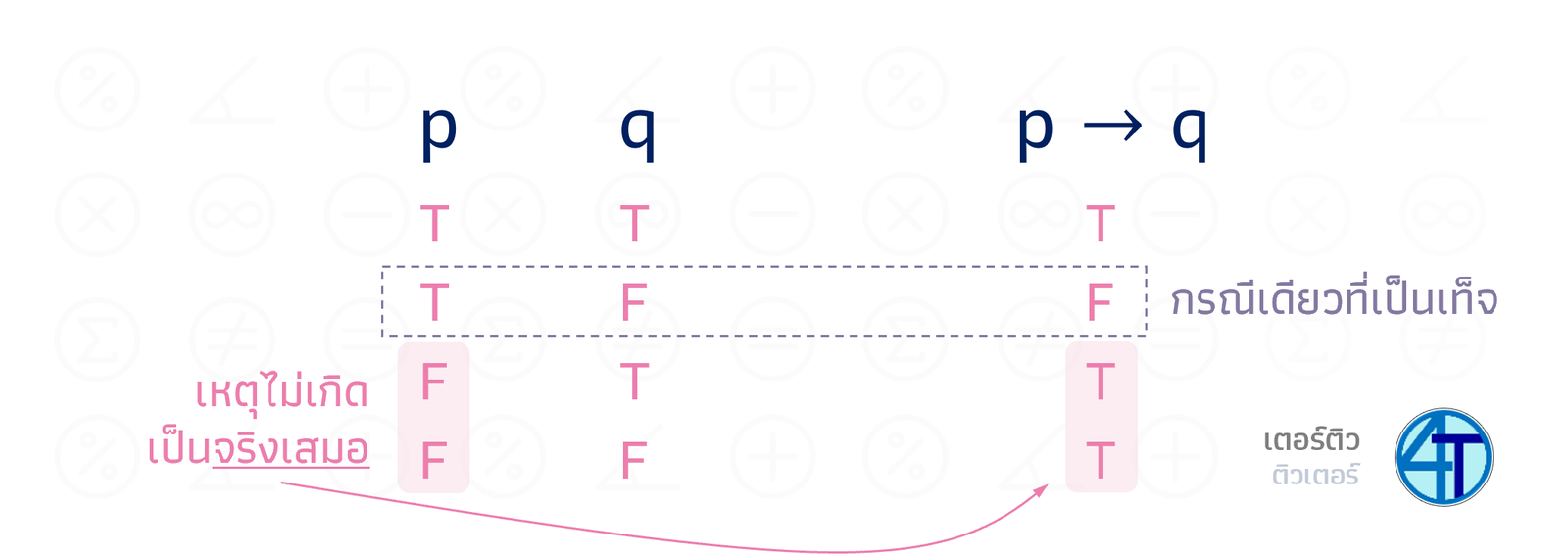
ประพจน์ที่มาเชื่อมกันด้วย "ถ้า ... แล้ว" จะมีความหมายในลักษณะของ เหตุ (เกิดขึ้นก่อน) และ ผล (เกิดตามมา) วิธีการเข้าใจง่าย ๆ คือ สมมติเรามี \(p\to q\) แปลว่า \(p\) เป็นเหตุ และ \(q\) เป็นผล

หาก เหตุเกิด (\(p\) เป็น จริง) แต่ ผลที่ตามมาไม่จริง (\(q\) เป็นเท็จ) การเชื่อมกันด้วย "ถ้า ... แล้ว" จะไม่เป็นจริง พูดง่าย ๆ อีกอย่างว่า ถ้า ตัวหน้าเป็น จริง แต่ ตัวหลัง เป็นเท็จ "ถ้า ... แล้ว" จะให้ค่าความจริงเป็น เท็จ

และถ้าเหตุไม่เกิดล่ะ (\(p\) เป็นเท็จ) กรณีแบบนี้เราจะไม่สนใจเลยครับน้อง และบอกว่า เป็นจริงเสมอ ประโยคที่เป็นประพจน์ แบบนี้ถ้าเชื่อมกันด้วย "ถ้า...แล้ว" และตัวหน้าเป็น เท็จ เราจะสรุปเลยว่า ค่าความจริงของการเชื่อมกันครั้งนี้ เป็น จริง หากสับสนลองดูตารางประกอบด้านล่าง

ตัวอย่าง ประโยคที่เป็นประพจน์ แบบ "ถ้า...แล้ว" เช่น "ถ้า \(1+1=3\) แล้ว กรุงเทพอยู่ภาคเหนือของประเทศไทย" ประโยคอาจจะดูแบบ ไม่เมคเซ้นส์เลยพี่ ใช่ครับ แต่มันก็หาค่าความจริงได้นะ

เหตุคือ "\(1+1=3\)" ซึ่งเป็น เท็จ ดังนั้น เราก็ไม่ต้องคิดและ เพราะถ้าตัวหน้าเป็น เท็จ คำตอบจะเป็น จริง เสมอ ดังนั้น ตัวอย่างประพจน์ข้างบนเป็น จริง

ก็ต่อเมื่อ \(\leftrightarrow\)

"ก็ต่อเมื่อ" เป็นตัวเชื่อมประพจน์ แบบที่ทั้งสองฝั่งต้องมีค่าความจริงเหมือนกัน กล่าวง่าย ๆ คือ ถ้า \(p\leftrightarrow q\) จะเป็นจริงได้ ก็คือในกรณี ที่ \(p\) และ \(q\) มีค่าความจริงเหมือนกัน เช่น \(p\) จริง \(q\) จริง หรือ \(p\) เท็จ \(q\) เท็จ

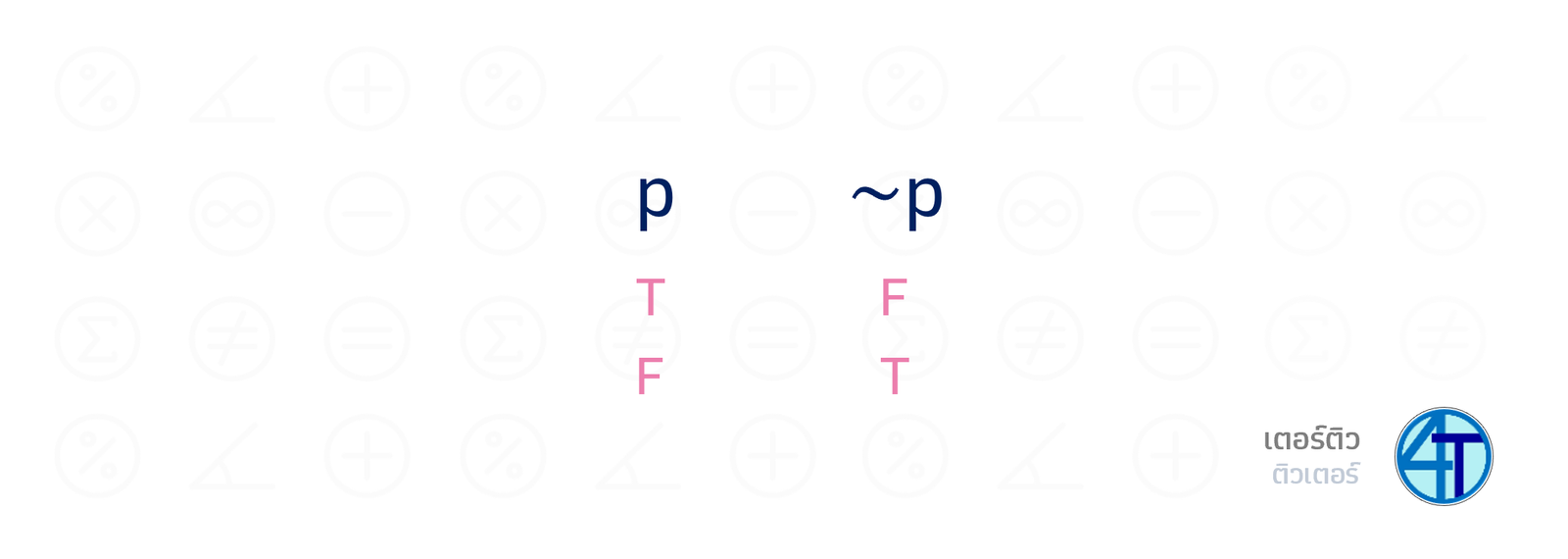
นิเสธ \(\sim\)

นิเสธ เป็นตัวที่ง่ายมาก คือ กลับค่าความจริง จากเท็จเป็นจริง และ จากจริงเป็นเท็จ ดังสรุปได้ตามตารางด้านล่าง ตัวอย่างเช่น นิเสธของประพจน์ "\(1+1=3\)" จะมีค่าความจริง เป็น จริง เพราะ ประพจน์ \(1+1=3\) เป็น เท็จ ดังนั้น นิเสธขิงมันเลยเป็น จริง

ดังนั้น สำคัญที่สุด ก่อนที่เราจะเข้าบทเรียนต่อไป ก็คือ น้อง ๆ จะต้องรู้ตารางที่พี่สอนไปข้างบนได้หมด ว่า ตัวเชื่อมประพจน์ แต่ละอัน เมื่อเจอ ประพจน์หนึ่งเป็น จริง/เท็จ อีกอันเป็น จริง/เท็จ ค่าความจริง (ผลลัพธ์) จะออกมาเป็นอย่างไร ตัวอย่างคร่าว ๆ มีดังนี้ (แต่น้องต้องจำให้ได้หมดนะ)

การหาค่าความจริงของประพจน์

พี่จะขอแบ่งออกเป็น 2 ประเภทใหญ่ ๆ ดังนี้

แบบ 1 บอกค่าความจริงของประพจน์ย่อย และ หาค่าความจริงประพจน์ใหญ่

เราจะมาดูตัวอย่างโจทย์กันว่า โจทย์สามารถออกแบบไหนได้บ้าง ในตัวเชื่อมที่สอนไปข้างบน เรื่อง ตัวเชื่อมประพจน์ เราได้รู้กันไปแล้วว่า แต่ละตัวเชื่อม จะได้คำตอบแบบไหนบ้าง ลองมาดูโจทย์ตัวอย่างเพื่อความเข้าใจ

สมมติโจทย์กำหนดให้ \(p\) เป็นจริง \(q\) เป็นจริง และ \(r\) เป็นเท็จ จงหาความจริงของประพจน์ต่อไปนี้

\((p\to q)\wedge r\)

การทำก็ทำเหมือนน้อง ๆ คิดเลขเลยครับ ค่อย ๆ ทำในวงเล็บก่อน เราต้องหา \(p\to q\) ซึ่ง \(p\equiv T\) และ \(q\equiv T\) (เครื่องหมาย สมมูล (\(\equiv\)) ที่พี่จะกล่าวต่อไปในพาร์ทท้ายสุดของบทนี้ ตอนนี้ขอยกมาก่อน เพื่อความง่ายในการเขียน มันแปลว่า "ค่าความจริงเหมือนกัน" น้องคิดง่าย ๆ เหมือนเครื่องหมาย "เท่ากับ" ก็ได้)

ดังนั้น \(p\to q\equiv T\to T\equiv T\) อันนี้ตรงตัวตามกฎของ "ถ้า...แล้ว" ใครยังจำไม่ได้ สามารถเปิดรูป สรุปตัวเชื่อมประพจน์ ประกอบไปได้ด้วยระหว่างการดูบทนี้นะ ดังนั้น ในวงเล็บเราก็จะได้ \(T\) พอมา "และ" กับ \(r\) ซึ่ง \(r\equiv F\) ดังนั้น \(T\wedge r\equiv T\wedge F\equiv F\)

โดยปกติการเขียนเป็นแผนภาพต้นไม้จะดูง่ายกว่า

ลองอีกตัวอย่าง ก่อนจะเข้าโจทย์ฝึกและกัน

กำหนดให้ \(p\) เป็นเท็จ จงหาค่าความจริงของประพจน์ \((q\vee r)\to((p\to q)\vee r)\)

อ่าวพี่ ทำไมโจทย์ให้มาแค่ ค่าความจริงของ \(p\) แต่โจทย์ถามประพจน์ที่มีทั้ง \(p, q, r\) เลยครับ ใช่แล้วน้อง มันจะมีโจทย์พิเศษแบบนี้แหละ เดี๋ยวเรามาดูกันว่าข้อนี้ทำไมถึงทำโจทย์ได้ โดยไม่ต้องบอก \(q\) กับ \(r\)

โจทย์บอกว่า \(p\equiv F\) เราลองแทนไปก่อนเลย

จาก \((q\vee r)\to((p\to q)\vee r)\) เป็น
\((q\vee r)\to((F\to q)\vee r)\) 

หากเราจำกันได้ "ถ้า ... แล้ว" ถ้าเหตุเป็น เท็จ ผลจะเป็นจริงเสมอ ดังนั้น ในวงเล็บก้อน \(F\to q\) ก็เลยเป็น จริง ไปเลย โดยที่เราไม่จำเป็นต้องรู้ค่าความจริงของ \(q\) เลยด้วยซ้ำ ดังนั้นตอนนี้โจทย์เลยกลายเป็น

\((q\vee r)\to(\textcolor{blue}{T}\vee r)\)

และเราก็รู้อีกว่า "หรือ" เนี่ย ถ้ามี ตัวใดตัวหนึ่งเป็นจริง ประพจน์นั้นก็จะเป็นจริงเลย โดยไม่ต้องไปสนใจตัวอื่นและ ดังนั้นแปลว่า \(\textcolor{blue}{T}\vee r\) ก็จะได้เป็น \(T\) ไปเลย โดยไม่ต้องรู้ค่าความจริงของ \(r\) เช่นเดียวกัน ดังนั้นตอนนี้โจทย์กลายเป็น

\((q\vee r)\to\textcolor{blue}{T}\)

หากน้องนึกดี ๆ "ถ้า ... แล้ว" ผลก็จริง จะมีสองกรณี (1) เหตุเป็น จริง (2) เหตุเป็น เท็จ แต่ทั้งสองกรณี ให้ค่าความจริงของ "ถ้า ... แล้ว" เป็นจริงทั้งคู่ ดังนั้น การที่ผลเป็นจริงใน "ถ้า ... แล้ว" เราจะสรุปได้ทันที่ว่า เป็นจริง โดยไม่ต้องสนใจตัวหน้า (เหตุ) เพราะฉะนั้นแปลว่า โจทย์ก็กลายเป็น

\(\textcolor{blue}{T}\)

ซึ่งจบแล้ว ตอบว่า เป็นจริง (หากใครอ่านแล้วมองไม่เห็นภาพ สามารถดู วิดีโอนาทีที่ 21:05 เดี๋ยวพี่จะเอาโจทย์นี้เข้าไปพูดในคลิปด้วย)

ดังนั้น อยากให้จำไว้เสมอว่า บางทีเราไม่จำเป็นต้องรู้ค่าความจริงทุกอย่างก็ได้ ก็สามารถตอบคำถามได้เหมือนกัน

แบบ 2 บอกค่าความจริงของประพจน์ใหญ่ และ หาค่าความจริงแต่ละตัว p q และ อื่น ๆ

ในเรื่องนี้เราจะพูดถึง การที่โจทย์ให้ค่าความจรืงของประพจน์ใหญ่มาอันเดียว และให้หาตัวย่อย โดยที่พี่จะโฟกัสแค่กรณีที่ มีค่าความจริงตัวย่อย เพียงชุดคำตอบเดียวเท่านั้น พูดง่าย ๆ ว่า แบบไม่กำกวม หรือ มีหลายคำตอบ

ตัวอย่าง ง่ายสุดคือ ถ้า \(p\vee q\) มีค่าความจริงเป็น เท็จ จงหาค่าความจริงของ \(p\) และ \(q\)

โจทย์ข้อนี้ หากน้องจำได้ในตาราง "หรือ" กรณีเดียวเลยที่ทำให้ \(p\vee q\) เป็นเท็จ ก็คือ กรณีที่ \(p\equiv F\) และ \(q\equiv F\) นั่นเอง ไม่กำกวม ดังนั้นข้อนี้ตอบ \(p\) เท็จ \(q\) เท็จ

ในบทนี้เราจะใช้ความ Unique (เป็นหนึ่งเดียว = มีกรณีเดียว) มาช่วยค่อนข้างเยอะ ตัวอย่างเช่น หากเราบอกว่า \(\heartsuit\to\square\) เป็นเท็จ เราสรุปได้ทันทีว่า \(\heartsuit\equiv T\) และ \(\square\equiv F\) เพราะมันมีกรณีเดียว

ดังนั้นไอเดียมันก็จะเหมือนกับพาร์ท 1) ที่น้องหาค่าความจริงของประพจน์ใหญ่นั่นแหละ แต่จะคิดกลับ ๆ ด้านกันเฉย ๆ งั้นลองไปทำโจทย์ ข้างล่างเลย ไม่ยากมาก แต่มีเกือบครบทุกองค์ประกอบที่น่าสนใจ