การดำเนินการของเซต \(\;\cap\;,\;\cup\;,\;-\;,\;^{\prime}\) 

เกริ่นนำ

ขอเกริ่นคร่าว ๆ กันก่อนและกันครับน้อง ๆ ว่า การดำเนินการของเซต เนี่ย มันคืออะไร ลองนึกภาพตามพี่ สมมติเรามีตัวเลข 2 ตัวเลข เลข \(5\) กับ \(10\) การที่น้อง ๆ นำ \(5+10\) ได้ผลลัพธ์ \(15\) หรือ \(5\times 10\) ได้ \(50\) อะไรก็ตามแต่ เครื่องหมาย บวก \(+\) หรือ คูณ \(\times\) อะไรพวกนี้นี่แหละที่เราเรียกว่า ตัวดำเนินการ แต่จากตัวอย่างด้านบนมันคือ การดำเนินการของตัวเลข

ดังนั้น การดำเนินการของเซต ก็จะเป็น เครื่องหมายการกระทำ ที่เรานำเซต 2 เซต มากระทำกัน และผลลัพธ์ก็ได้เป็น เซตใหม่ นั่นเอง ทีนี้เราไปดูกันเลยครับว่า การดำเนินการของเซต มีอะไรกันบ้าง

อินเตอร์เซค (Intersect) \(\cap\)

สมมติพี่มี เซต \(A\) กับเซต \(B\) หากพี่ต้องการนำมาอินเตอร์เซคกัน \(A\cap B\) มันหมายความว่าพี่จะได้ผลลัพธ์เป็นเซตใหม่ที่ สมาชิกอยู่ทั้งใน \(A\) และ ใน \(B\) บางคนอาจจะเรียกว่ามันคือการดึงเอา สมาชิกร่วม เพื่อให้เห็นภาพมากยิ่งขึ้น ตัวอย่าง \(A=\{1,2,\textcolor{red}{3}\}\) และ \(B=\{\textcolor{red}{3},4,5\}\) น้อง ๆ จะสังเกตเห็นว่า สมาชิกร่วม มีแค่เลข 3 เท่านั้น ที่อยู่ทั้งในเซต \(A\) และเซต \(B\) ดังนั้น \(A\cap B = \{\textcolor{red}{3}\}\)

ระวังนิดนึงว่า คำตอบของ การดำเนินการของเซต ยังเป็นเซตอยู่นะ สังเกตว่าพี่ยังใส่ \(\{\) และเครื่องหมาย \(\}\) ครอบเลข \(3\) อยู่ในตัวอย่างด้านบน แปลว่าผลลัพธ์คือ เซตที่มี \(3\) เป็นสมาชิก

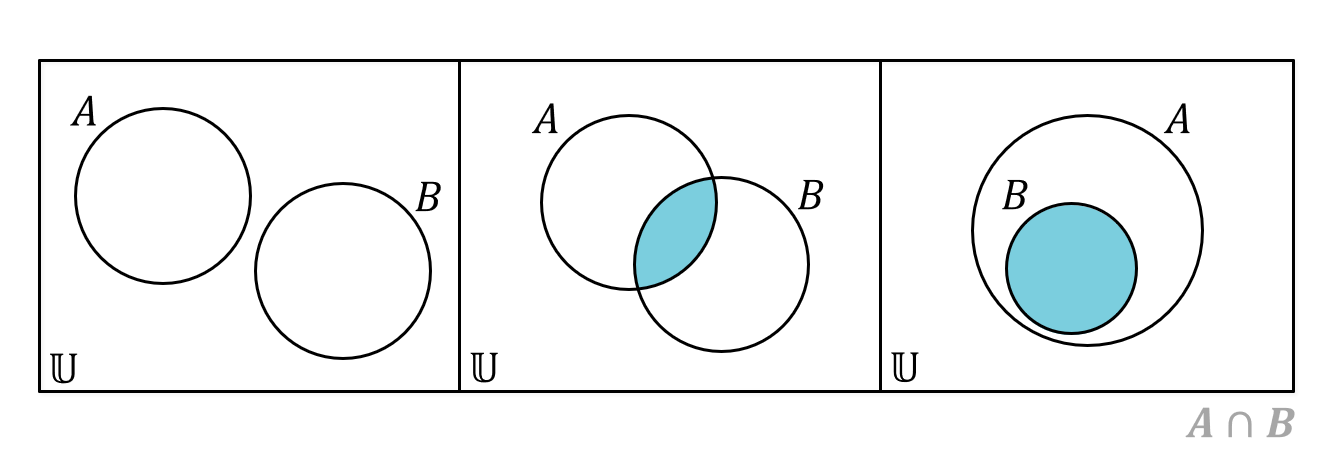
หากพูดถึง แผนภาพเวนน์ ออยเลอร์ แล้วหล่ะก็ ไม่ยากเลยเพราะส่วนที่เราต้องการก็คือส่วนที่ อยู่ทั้งใน \(A\) และ \(B\) ลองดูตัวอย่างแบบต่าง ๆ ตามภาพด้านบนเพื่อความเข้าใจที่มากขึ้นได้เลยครับ

ยูเนี่ยน (Union) \(\cup\)

เช่นเคยครับน้อง ๆ สมมติพี่มี เซต \(A\) กับเซต \(B\) หากพี่ต้องการนำมายูเนี่ยนกัน \(A\cup B\) มันหมายความว่าพี่จะได้ผลลัพธ์เป็นเซตใหม่ที่ สมาชิกอยู่ใน \(A\) หรือ ใน \(B\) บางคนอาจจะเรียกว่ามันคือการดึงเอา สมาชิกทั้งหมดมารวมกัน เพื่อให้เห็นภาพมากยิ่งขึ้น ตัวอย่าง เซตเดิมกับอันที่แล้ว \(A=\{1,2,3\}\) และ \(B=\{3,4,5\}\) น้อง ๆ จะสังเกตเห็นว่า หากเรานำสมาชิกมารวมกันทั้งหมด ก็จะมี \(1,2,3,3,4,5\) ซึ่งปกติแล้วเรื่องเซต หากเจอตัวซ้ำ ในกรณีนี้ คือ เลข \(3\) ซ้ำ เราก็จะนับแค่ตัวเดียว ดังนั้น \(A\cup B = \{1,2,3,4,5\}\)

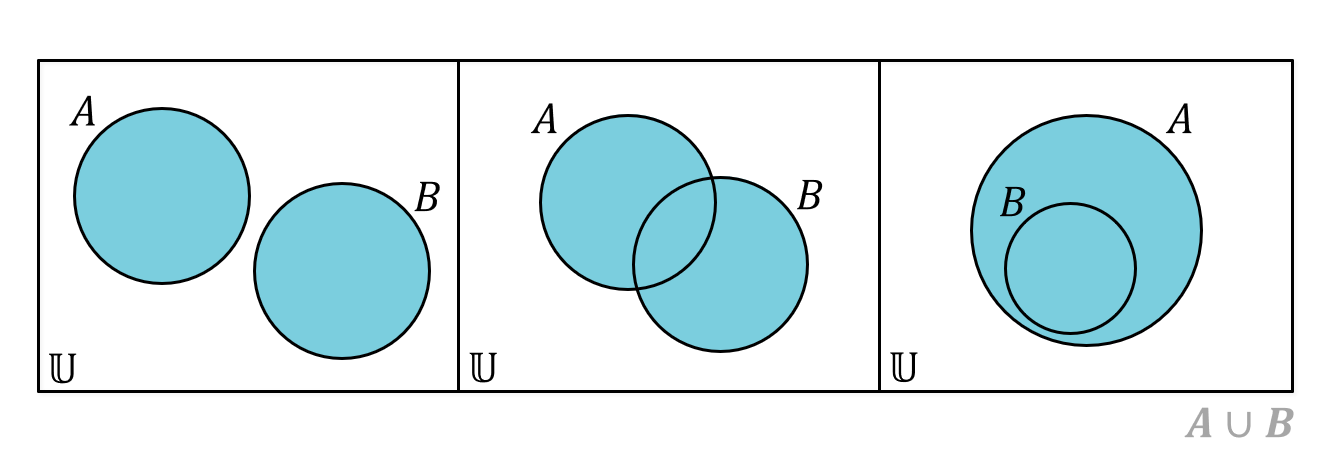
หลักการก็คือเอาสมาชิกมารวมกัน ก็คือการที่ไม่ว่าสมาชิกจะ (1) อยู่แค่ใน \(A\) (2) อยู่แค่ใน \(B\) หรือ (3) อยู่ทั้งใน \(A\) และ \(B\) ก็เอามาหมดเลย

ผลต่าง (Difference) \(-\)

การดำเนินการของเซตนี้ทำงานเหมือนกับ "การลบ" เลย ง่ายๆ ให้นึกถึงเครื่องหมายลบเลข สมมติเรามี 5 - 2 สิ่งที่เราต้องทำก็คือ นำ 5 ตั้งต้น และหักออกไปสอง ไอเดียเรื่องเซตก็เหมือนกันเลย คือถ้าเรามี \(A-B\) เราก็จะนำเซต \(A\) ตั้งต้น จากนั้น หักส่วนที่อยู่ใน \(B\) ออก

ตรงไหนของ \(A\) ที่อยู่ใน \(B\) เราก็จะลบออก

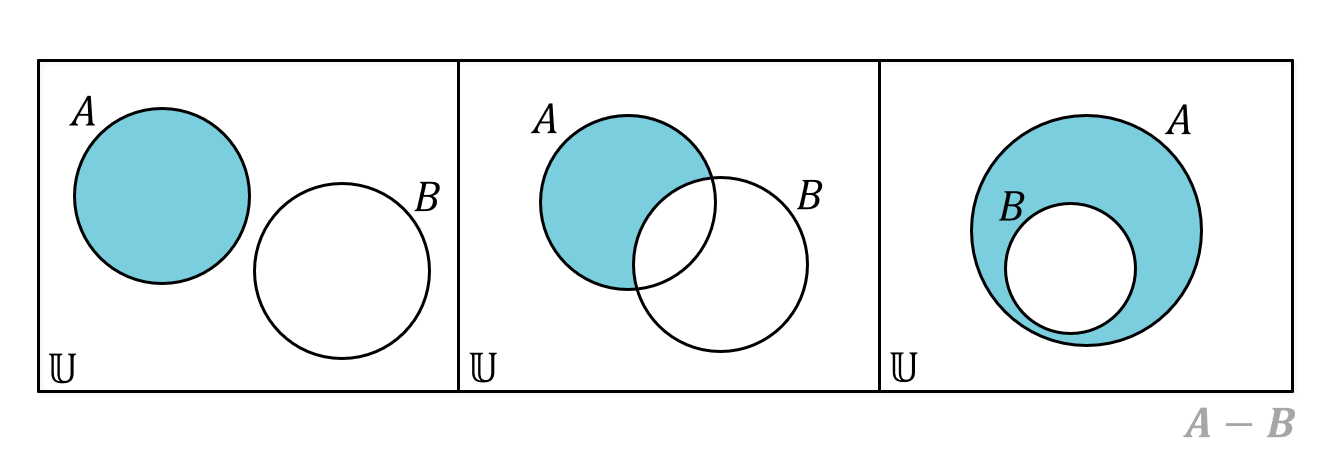
ทั้งหมดที่แรเงาด้านบน หากน้อง ๆ สังเกต มันคือบริเวณที่อยู่ใน \(A\) แต่ไม่อยู่ใน \(B\) ทั้งหมดเลย

วิธีการหา \(A-B\)  ที่แนะนำ คือ ให้ไล่เช็คสมาชิกที่อยู่ใน \(A\) หากตัวไหนอยู่ใน \(B\) เราจะตัดมันออก ตัวอย่าง กำหนดให้ \(A=\{1,2,3,4\}\) และ \(B=\{3,5\}\) หากต้องการหา \(A-B\)   ให้น้อง ๆ ไล่ทุกตัวใน \(A\) จะสังเกตว่า มีแค่ \(3\) เท่านั้นที่อยู่ใน \(B\) ด้วยดังนั้นเราต้องตัด \(3\) ออกจาก \(A\) คำตอบจึงเป็น \(\{1,2,4\}\)

จริงหรือเท็จ หาก \(A-B=\varnothing\) แล้ว \(A=B\)

เฉลย

ข้อนี้บางคนอาจจะคิดเหมือนเครื่องหมายลบ แบบ \(a-b=0\) ถ้าย้ายข้างไปก็ได้ \(a=b\) แต่จริงๆแล้ว ในเรื่องเซตเราต้องระวังกันอย่างมากเลย เครื่องหมายลบถึงมันจะทำงานคล้าย ๆ กับการลบเลข

หากคิดดี ๆ แล้วในกรณีที่ \(A\subset B\) ทุกสมาชิกของ \(A\) อยู่ใน \(B\) ดังนั้น เราต้องตัดทิ้งทั้งหมด แสดงว่า \(A-B=\varnothing\) แต่ \(B\) ไม่จำเป็นต้องเท่ากับ \(A\) ก็ได้ อย่างในกรณีคือ \(B\) คลุม \(A\) อยู่

ดังนั้น ตอบว่าเท็จ เพราะ \(A-B=\varnothing\) ก็ต่อเมื่อ \(A\subseteq B\)

คอมพลีเมนต์ \(\prime\)

เช่น \(A^{\prime}\) ก็หมายความว่าเอาที่ไม่อยู่ใน \(A\)

การถามหาคอมพลีเมนต์เราสามารถใช้สัญลักษณ์ได้สองแบบ อย่างแรกคือ \(A^{\prime}\) อีกอันคือ \(A^{c}\) หลักการหาง่ายๆ ให้เราใช้ไอเดียของ ผลต่าง จากหัวข้อที่แล้ว การที่เราบอกว่า \(A^{\prime}\) นั่นหมายความว่า เราเอาสมาชิกที่ไม่อยู่ใน \(A\) ถ้าเรามองออกก็จบ แต่ถ้าคิดแบบง่ายๆ ก็คือการที่เรานำ \(\mathbb{U}-A\) นั่นเองครับน้องๆ เรานำเอกภพสัมพัทธ์ตั้งต้น และลบทุกอย่างใน \(A\) ออกก็ได้เหลือ สิ่งที่ไม่อยู่ใน \(A\)

ฝึกแรเงา แผนภาพเวนน์ ออยเลอร์ จากสมการตัวดำเนินการของเซต

หัวข้อนี้จะเป็นการฝึกแรเงาตามสมการตัวดำเนินการหลาย ๆ ตัวมารวมกันเช่น \((A\cap B)^{\prime}\) หรือ \(A^{\prime}-B\) อะไรแบบนี้ ซึ่งพี่จะขอรวมหัวข้อนี้รวมกับวิดีโอสอนฝึกแรเงา (นาทีที่ 11) ด้านบนไปเลยนะ เนื่องจาก น้อง ๆ จะสามารถเข้าใจได้ง่ายมากขึ้น หากใช้คำพูดและแอนิเมชั่นเข้ามาช่วย

แต่หากให้พูดเกริ่นๆ ก่อนก็คือ เรามีสองวิธี

• (1) ค่อยๆ แรเงาทีละส่วนของสมการและนำมารวมกันจนเสร็จ
• (2) เขียนแผนภาพเวนน์ ออยเลอร์ ออกเป็นเซตซึ่งประกอบไปด้วย Regions ไหนบ้างและจากนั้น แก้สมการโดยการใช้เซตแทนการระบายสี เมื่อเสร็จค่อยนำคำตอบไปแรเงา