ทฤษฎีบทเศษเหลือ และ การแยกตัวประกอบพหุนาม ม.4

พหุนามที่สามารถแยกตัวประกอบโดยไม่ต้องตั้งหาร (ทวน ม.ต้น)

อย่าลืมว่าเรามีพหุนามดีกรีมากกว่าสองหลากหลายประเภทที่น้องไม่ต้องแยกตัวประกอบแบบ ตั้งหารอย่างเดียว ซึ่ง เรื่องนี้เป็นเรื่องที่น้องเจอกันแล้วใน ม.3 ใน เรื่อง การแยกตัวประกอบของพหุนามที่มีดีกรีสูงกว่าสอง (ยังไม่มีบทความนี้) ดังนั้น มันไม่จำเป็นว่า เราจะต้องตั้งหารเสมอไป หากดีกรีมากกว่าสอง

การแยกตัวประกอบพหุนาม

เกริ่นกันสักนิดว่า เรื่องนี้สุดท้ายแล้วมันจะไปช่วยเรา ในการ แก้สมการและอสมการ ที่เราจะเรียนกันในบทต่อ ๆ ไป ของจำนวนจริง ม.4 เพราะหากเรา พหุนามดีกรีก้อนใหญ่ เราจะไม่สามารถทำอะไรมันต่อได้เลย ยกเว้นการแยกตัวประกอบและพยายาม จัดรูปหรือตัดทอน

ตัวอย่าง หากเรามี พหุนาม \(\dfrac{x^3-4x^2+6x-24}{x-4}\) เมื่อ \(x\ne 4\) น้องจะจัดรูปทำอะไรต่อไม่ได้เลย แต่หากเราสามารถแยกตัวประกอบได้ว่า ตัวข้างบนคือ \(x^3-4x^2+6x-24=(x-4)(x^2+6)\) นะ เราจะได้พหุนามดังรูป \(\dfrac{(x-4)(x^2+6)}{x-4}\) และ เราสามารถตัด \(x-4\) บนล่างได้ ดังนั้น ก็เหลือแค่ \(x^2+6\) สังเกตดูไอเดียเฉย ๆ นะว่า มันมีประโยขน์ในการแก้สมการแน่นอน ดังนั้นไปเริ่มกันเลย

ถ้าเป็น เรื่อง การแยกตัวประกอบพหุนามดีกรีสอง น้อง ๆ ได้เรียนกันไปแล้วตั้งแต่ ม.2 บอกตรงนี้เลยว่าถ้าใครไม่คล่อง คือต้องกลับไปฝึกด่วน ๆ เลย เพราะไม่งั้น น้องไม่มีทาง ทำโจทย์สอบ Entrance ได้เร็วแน่นอน

ในบทนี้เราจะเน้นการแยกตัวประกอบ พหุนาม ดีกรี 3 ขึ้นไป กัน โดยเราจะใช้ การหารสังเคราะห์ เข้ามาช่วย เพื่อความรวดเร็ว ก่อนอื่น น้องต้องเข้าใจไอเดียก่อนว่า

ดังนั้น หากเรา (จากตัวอย่างด้านบน) ว่า \(x^3-4x^2+6x-24=(x-4)(x^2+6)\) มันแปลว่า \(x-4\) เป็นตัวประกอบของ \(x^3-4x^2+6x-24\) เพราะมันไม่มีเศษ ให้สังเกตตรงเศษ 0 ให้ดี ๆ เพราะเราจะนำการหารสังเคราะห์มาช่วยดูเศษ

ก่อนไป ยกตัวอย่างเพิ่มอีกสักนิด สมมติ เรามี \(x^3-5x^2-x+5=(x-1)(x+1)(x-5)\) แปลว่า ทั้งสามตัวเป็นตัวประกอบ ของ \(x^3-5x^2-x+5\) เพราะมันไม่มีเศษเหลือ ดังนั้น

ให้ \(x^3-5x^2-x+5\) เป็นตัวตั้ง และ แต่ละตัวเป็นตัวหาร เช่น \(x-1\) เวลาเราหารสังเคราะห์มันจะได้เศษเป็น \(0\) นั่นเอง

เช่น ตัวตั้ง \(x^3-5x^2-x+5\) ตัวหาร \(x-1\)

ดังนั้นหลักการแยกตัวประกอบของดีกรีสามขึ้นไป แบบหารตรง ๆ มีขั้นตอนดังนี้

ทำไมต้องใช้ตัวประกอบของพจน์หลังสุดไปลอง ? หากน้องสังเกตดี ๆ พจน์หลังสุดที่เป็นค่าตัวเลข มันจะเกิดจาก ตัวเลขข้างหลังคูณกันทั้งหมด เช่น \(x^3-5x^2-x\textcolor{blue}{+5}\) \(=(x\textcolor{blue}{-1})(x\textcolor{blue}{+1})(x\textcolor{blue}{-5})\)  เราจะได้ว่า \(+5=(-1)(+1)(-5)\) หรือ อีกตัวอย่าง \(x^4+2x^3-21x^2-22x\textcolor{blue}{+40}\)  \(=(x\textcolor{blue}{+2})(x\textcolor{blue}{-1})(x\textcolor{blue}{-4})(x\textcolor{blue}{+5})\)  เราจะได้ว่า \(+40=(+2)(-1)(-4)(+5)\)

ดังนั้น เราจะไม่แทนสุ่มมั่ว ๆ แต่เราจะเอาแค่ตัวประกอบของพจน์หลังมาแทน ถ้าเจอเศษ \(0\) ก็จะนำผลหารที่ได้ ไปแยกตัวประกอบต่อ

ก่อนจะไปฝึกแยกตัวประกอบ เราจะไปพูดถึง ทฤษฎีบทเศษเหลือ กันก่อน เนื่องจากหากน้อง ๆ สังเกต การหาตัวประกอบ คือการหารสังเคราะห์ และเศษเหลือ \(0\) แต่การหารสังเคราะห์ถึงมันจะไม่ได้ยาก แต่ถ้าเรา ต้องการรู้แค่เศษเหลือ มันมีวิธีที่เร็วกว่า นั่นก็คือใช้ ทฤษฎีบทเศษเหลือ

ทฤษฎีบทเศษเหลือ

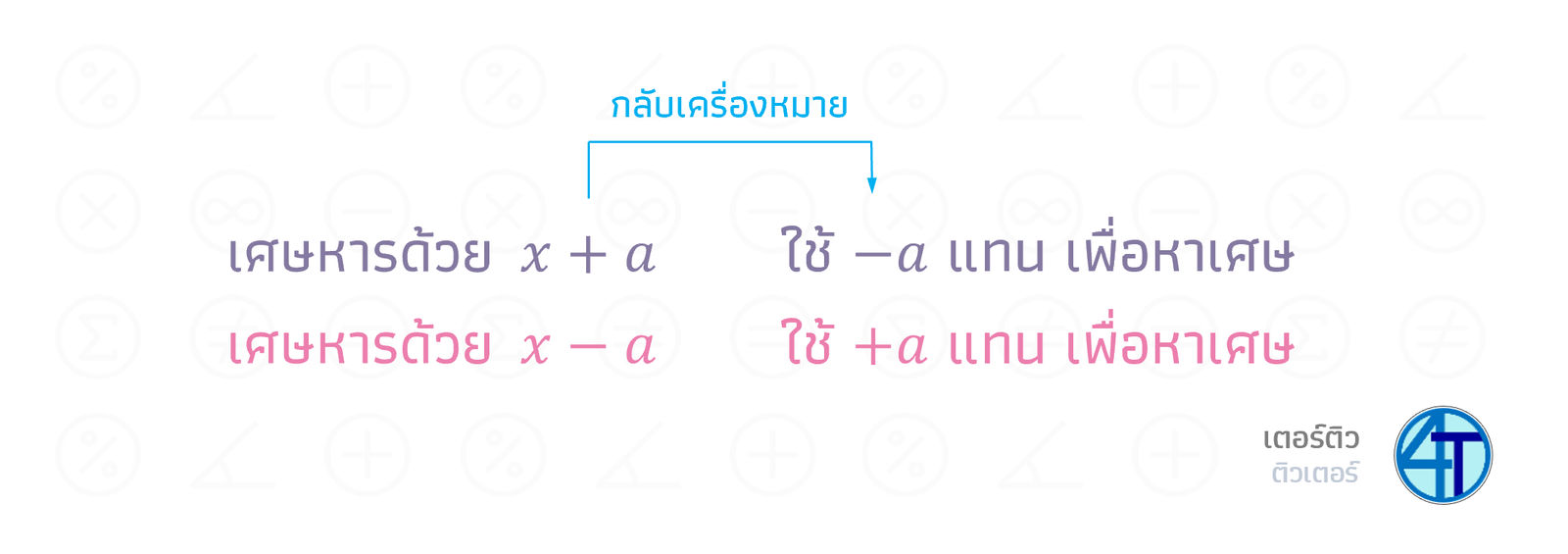
หากเราต้องการรู้เศษของการหารด้วย \(x+a\) ให้ใช้พจน์หลังกลับเครื่องหมาย แล้วนำไปแทนเป็น \(x\) จะได้เศษทันที ในกรณีนี้ต้องแทน \(-a\) ถ้าหากต้องการหาผลหารของ \(x-a\) ก็ต้องใช้ \(a\) ในการแทน

ตัวอย่างเช่น หาเศษของการหารพหุนาม \(x^2+3x-2\) ด้วย \(x-1\) ถ้ามองพหุนามเป็น \(P(x)\) เศษก็คือ แทน \(1\) (พจน์หลัง \(x-1\) คือ \(-1\) ต้องกลับเครื่องหมาย กลายเป็น \(1\)) เข้าไปในพหุนาม ก็คือ หา \(P(1)\) นั่นเอง

\(P(1)=1^2+3(1)-2=2\) ดังนั้น เศษคือ \(2\)

ตัวอย่าง ผลหารของ \(x^2+kx-2\) ด้วย \(x-4\) ได้ \(22\) จงหา \(k\)

ข้อนี้บอกเราว่า \(P(x)=x^2+kx-2\) และ \(P(4)=22\) นะ ดังนั้นลองแทน \(4\) ในพหุนาม เราจะได้ \(4^2+k(4)-2=22\) แก้สมการปกติเลย จะได้ว่า \(k=2\)

โจทย์การแยกตัวประกอบพหุนาม แบบหารตรง ๆ

จงแยกตัวประกอบของ \(x^3+2x^2-13x+10\)

ข้อนี้เราจะหาดูก่อนว่า ตัวไหนเศษเป็น \(0\) โดยเราจะเช็คแค่ ตัวประกอบพจน์หลังสุด ใส่ \(\pm\) ดังนั้น ตัวประกอบของ \(10\) ใส่บวกลบ คือ \(\pm1,\pm2,\pm5,\pm10\)

การหาเศษเราจะยังไม่หารสังเคราะห์เพราะเผื่อเศษไม่เป็น \(0\) ก็แปลว่าเราเปลืองเวลาหารสังเคราะห์ไปฟรี ๆ ดังนั้น จะใช้ ทฤษฎีบทเศษเหลือ ที่เล่าไปแล้วด้านบน แทน \(P(x)=x^3+2x^2-13x+10\) 

เราจะนำ \(\pm1,\pm2,\pm5,\pm10\) ไปแทนเป็น \(x\) ใน \(P(x)\) เพื่อดูว่าอันไหนได้เศษ \(0\) ลองเลข \(1\) จะได้ว่า \(P(1)=1^3+2(1^2)-13(1)+10\) \(=1+2-13+10=0\)  

ดังนั้นแปลว่า \(x-1\) เป็นตัวประกอบของ \(P(x)\)

ดังนั้นเราจะนำ \(x-1\) ไปหารสังเคราะห์ โดยมี \(x^3+2x^2-13x+10\) เป็นตัวตั้ง

จากหารสังเคราะห์จะเห็นว่า เศษเป็น \(0\) ตามที่เราคิดในผลหาร ใน ทฤษฎีบทเศษเหลือ และผลหาร คือ \(x^2+3x-10\) (จากหารสังเคราะห์ข้างบน ใครงงว่าผลหารดูจากหารสังเคราะห์ยังไงสามารถดูที่ เรื่องการหารสังเคราะห์ นะ)

ดังนั้น เราเขียนได้ว่า \(x^3+2x^2-13x+10\) \(=(x-1)(x^2+3x-10)\)  เมื่อได้ผลหารดีกรีสองเมื่อไหร่ เราจะใช้ การแยกตัวประกอบพหุนามดีกรีสอง ปกติทำเลย ดังนั้น \(x^3+2x^2-13x+10\) \(=(x-1)\textcolor{blue}{(x^2+3x-10)}\) \(=(x-1)\textcolor{blue}{(x+5)(x-2)}\) 

ทฤษฎีบทตัวประกอบ

อย่างที่บอกว่าการแยกตัวประกอบคือ

1. หาตัวที่เศษจากการหารได้ \(0\) จาก ทฤษฎีบทเศษเหลือ
2. นำไปหารสังเคราะห์ และวนซ้ำเรื่อย ๆ จนเหลือดีกรี 2 แล้วก็แยกตัวประกอบธรรมดา

แต่ในพาร์ทที่แล้วเราแยกตัวประกอบแค่พหุนามดีกรีสูงที่ สัมประสิทธิ์พจน์หน้า คือ \(1\) ตัวอย่าง \(x^3+\dots\) หรือ \(x^4+\dots\)

ในตอนนี้เราจะมาดูกันว่า ถ้าพหุนามมันมีสัมประสิทธิ์ที่ ไม่ใช่ 1 ในดีกรีสูงสุดจะทำยังไง เช่น \(2x^3+3x^2-5x-6\)

เราจะทำคล้ายเดิมคือ นำตัวประกอบของพจน์หลังสุด ใส่บวกลบ มาหาเศษ แต่จะเปลี่ยนนิดหน่อย คือ

เราจะหารด้วย สปส.พจน์ดีกรีสูงสุดด้วย (จริง ๆ มันก็แบบเดียวกันกับตอนที่เราเรียนข้างบนตอน สปส.พจน์ดีกรีสูงสุดเป็น 1 เราจะหารด้วย 1 มันก็เลยเหลือแค่ \(\pm\)ตัวประกอบพจน์ค่าคงที่)

ขั้นแรก เราก็มาฝึกหากลุ่มตัวเลขที่ต้องเอาไปแทน \(P(x)\) ในทฤษฎีบทเศษเหลือ กันก่อน ตัวอย่างเช่น \(6x^3+5x^2-8x-3\)  เราจะต้องนำ \(\pm\dfrac{1,3}{1,2,3,6}\) มาแทน จับทุกคู่ก็จะได้ เริ่มที่เศษเป็น \(1\) ก่อน \(\pm1,\pm\dfrac{1}{2},\pm\dfrac{1}{3},\pm\dfrac{1}{6}\) และเศษเป็น \(3\) จะได้ \(\pm3,\pm\dfrac{3}{2}\) ที่พี่ข้าม \(\pm\dfrac{3}{3}=\pm1,\) กับ \(\pm\dfrac{3}{6}=\pm\dfrac{1}{2}\) เพราะมันมีอยู่แล้วตอนเราคิดเศษเป็น \(1\) 

สำหรับ \(6x^3+5x^2-8x-3\) สรุปมีเลขที่ต้องไปแทน ดังนี้ \(\pm1,\pm\dfrac{1}{2},\pm\dfrac{1}{3},\pm\dfrac{1}{6},\pm3,\pm\dfrac{3}{2}\) 

พอเราได้ตัวเลขแล้ว ก็นำไปแทนใน \(P(x)\) หาว่าตัวไหนเป็นตัวประกอบ สังเกตว่า \(P\left(-\dfrac{1}{3}\right)=6\left(-\dfrac{1}{3}\right)^3+5\left(-\dfrac{1}{3}\right)^2\) \(-8\left(-\dfrac{1}{3}\right)-3\)  \(=0\)  

ดังนั้นแปลว่า มี \(x+\dfrac{1}{3}\) เป็นตัวประกอบ

เราจึงนำ \(x+\dfrac{1}{3}\) ไปหาร \(6x^3+5x^2-8x-3\) ได้ตามนี้

\( \begin{array}{c|rrrrr}-\dfrac{1}{3}&6&5&-8&-3\\&&-2&-1&3\\\hline\\&6&3&-9&0\end{array} \)

ดังนั้นผลหารคือ \(6x^2+3x-9\) เราจึงนำไปแยกตัวประกอบต่อจะได้ว่า \(6x^2+3x-9=3(2x^2+x-3)\) \(=3(2x+3)(x-1)\)  

ดังนั้นรวมร่างกันจะได้ว่า \(6x^3+5x^2-8x-3\)  \(=(x-\dfrac{1}{3})(3)(2x+3)(x-1)\) นำ \(3\) คูณเข้าไปในวงเล็บที่เป้นเศษส่วนเพื่อทำให้ไม่ติดเศษส่วน คำตอบเราก็คือ \(=(3x-1)(2x+3)(x-1)\)