อสมการพหุนาม ม.4

เลือกอ่านตามหัวข้อ?

- รู้จักความไม่เท่ากับ และ คำตอบของอสมการ (ช่วงปิด-เปิด)

อยากดูแบบวิดีโอ? (อยู่ระหว่างการจัดทำคลิป)

คำตอบของอสมการ

เราเคยเรียนไปแล้วในเรื่อง อสมการ ม.3 ว่าเครื่องหมายมีกี่แบบยังไงบ้าง ซึ่งการแก้อสมการสมัย ม.ต้นที่เราเรียนก็จะมีไอเดียหลัก ๆ คือ

1. คูณหารจำนวนลบ ต้องกลับเครื่องหมาย
2. คูณไขว้ก้อนที่ติดตัวแปรไม่ได้ เพราะว่า เราไม่รู้ว่ามันบวกหรือลบ

และคำตอบของอสมการ เราจะตอบติดเป็นช่วงของคำตอบ ตอน ม.ต้น เราเรียนเกี่ยวกับการเขียนคำตอบคร่าว ๆ กันไปแล้ว ที่เป็นเรื่องจุดโปร่งจุดทึบ ใครสนใจทวน สามารถไปดูได้ที่เรื่อง อสมการ ม.3 เลยนะครับ

ใน ม.4 เราจะให้นิยามเพิ่ม ในการเขียนรูปแบบคำตอบ คือ ช่วงเปิด และ ช่วงปิด

ช่วงเปิด \((\) = ไม่เอา = จุดโปร่ง
ช่วงปิด \([\) = เอา = จุดทึบ

เราไปดูตัวอย่างกันก่อน เพื่อความเข้าใจง่าย และเดี๋ยวสรุปตบท้ายไปอีกที สมมติว่าเรามี คำตอบของอสมการตามรูปแบบด้านล่าง

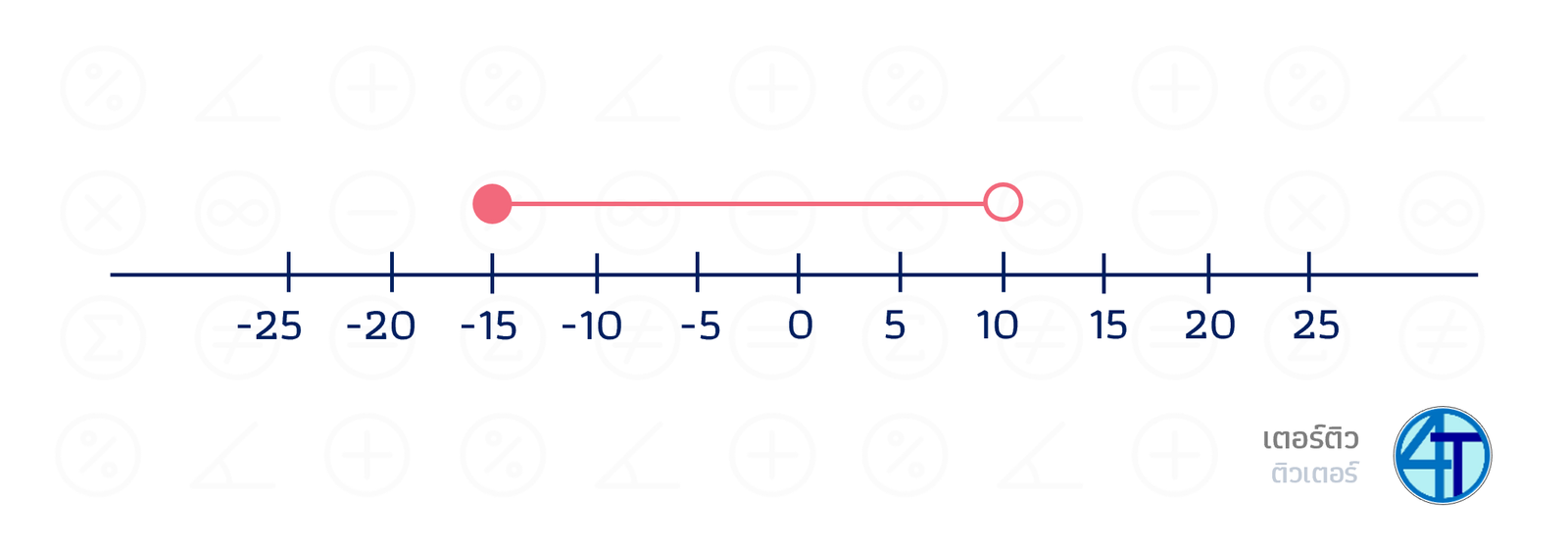
แบบนี้เราจะบอกว่า \(-15\) ถึง \(10\) โดยที่ เอา \(-15\) แต่ ไม่เอา \(10\) จะเขียนได้ว่า \(-15\le x\lt 10\)

การเขียนคำตอบแบบช่วง เราจะเขียนว่า

\([-15,10)\)

อีกตัวอย่าง หากเราบอกว่า \(x\lt 3\) หล่ะ แบบนี้สังเกตว่าฝั่งซ้ายมันไปเรื่อย ๆ ไม่รู้จบเลย เราจะเรียกว่า ไปจนถึงลบอินฟินิตี้ (ค่าน้อยสุด) สัญลักษณ์ \(-\infty\) เราก็จะได้ช่วงแล้วว่า คำตอบคือ \(-\infty\) ถึง \(3\)

การเขียนคำตอบแบบช่วง เราจะเขียนว่า

\(\textcolor{blue}{(}-\infty,3)\)

\(\infty\) จะเป็น ช่วงเปิดเสมอ

จงเขียนคำตอบในรูปแบบช่วงของ \(x\gt 2\)

เฉลย

จงเขียนคำตอบในรูปแบบช่วงของ \(x\gt 2\) หรือ \(-5\le x\lt 2\)

เฉลย

จงเขียนคำตอบในรูปแบบช่วงของ จำนวนจริงทั้งหมด ยกเว้น \(0\)

เฉลย

คำตอบของเซต สามารถมีหลายช่วงได้ด้วย อย่างเช่นในตัวอย่างด้านบน ที่เราเขียน \(\cup\) (ยูเนี่ยน) เข้าไปช่วย ดังนั้น อีกคอนเซ็ปต์ที่น้องต้องคล่องคือ การนำช่วงคำตอบมา ยูเนี่ยนและอินเตอร์เซต กัน

ยูเนี่ยน และ อินเตอร์เซค ของช่วงคำตอบ

การทำโจทย์ในอนาคต เราอาจจะเจอโจทย์ถามให้นำช่วงคำตอบมา "และ" กัน หรือมา "หรือ" กัน หรือไม่ก็ในโจทย์ข้อเดียวนี่แหละ เราต้องมีการแบ่งกรณี (เช่นบทต่อไปในเรื่อง อสมการค่าสัมบูรณ์) ดังนั้น แม้แต่ในโจทย์หนึ่งข้อ เราก็อาจจะมีหลายช่วงคำตอบที่ต้องนำมา กระทำกัน หลักการก็เหมือนเรื่องเซตครับ คือ

อินเตอร์เซค เอา ที่มีร่วมกัน
ยูเนี่ยน เอา มารวมกัน

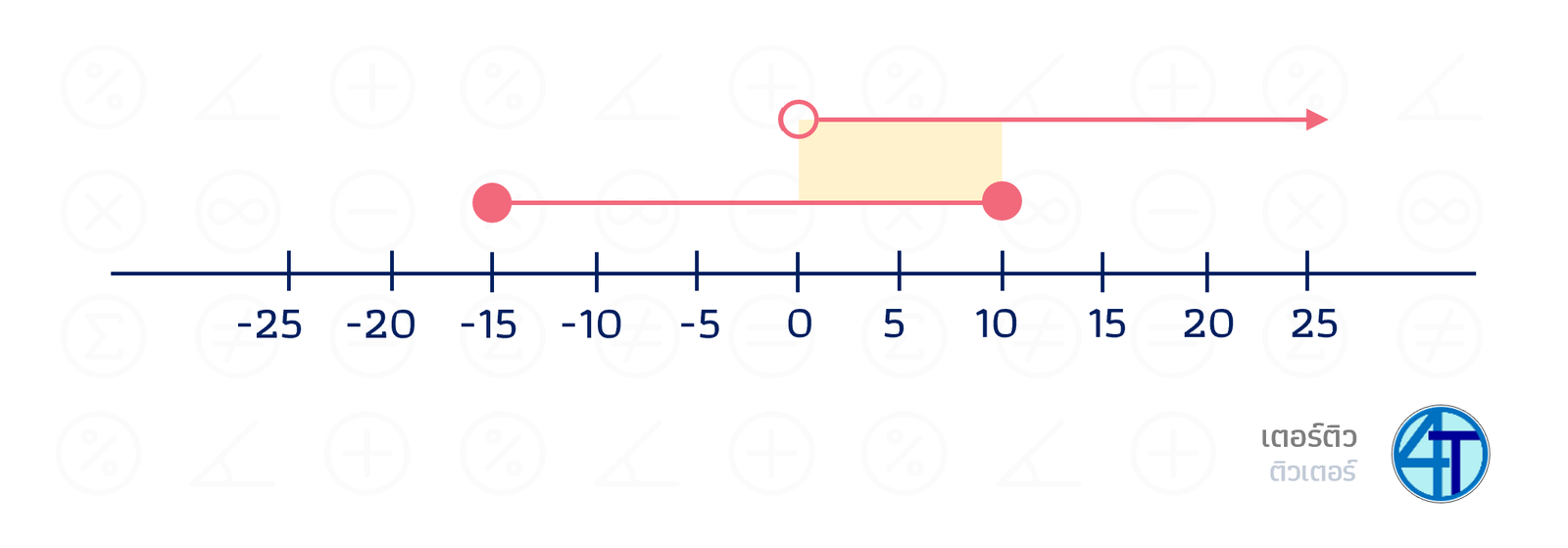
ถ้าเราจะนำช่วงทั้งอันบนมา \(\cap\) กัน จะได้ว่า \([-15, 10]\cap(0,\infty)\)

หลักการก็คือ ต้องหาส่วนที่มัน ซัอนทับกันอยู่ แปลว่ามีร่วมกัน ซึ่งคือส่วน \(0\) ถึง \(10\) นั่นเอง จากนั้น เราต้องวิเคราะห์จุดปลายอีกทีนึง เริ่มที่ปลายซ้าย (เลข \(0\)) เรารู้ว่า เส้นบนไม่มี \(0\) ดังนั้น ถ้ามาอินเตอร์เซคกัน ก็จะไม่มี \(0\) ติดมา ส่วน \(10\) มีทั้งตัวบนและล่าง ดังนั้น \(10\) เราจะเอา เพราะอยู่ทั้งคู่ เราเลยได้

\([-15, 10]\cap(0,\infty)=(0, 10]\)

ถ้าเราจะนำมา ยูเนี่ยน กัน \([-15, 10]\cup(0,\infty)\) ก็ต้องเอาส่วนที่มีทั้งหมดมารวมกัน ได้ว่ายาวตั้งแต่ \(-15\) ถึง \(\infty\) ก็จะเขียนได้ว่า \([-15, \infty)\)

จงเขียนคำตอบสำเร็จในรูปแบบช่วงของ \((-\infty,5]\cup[5,\infty)\)

เฉลย

จงเขียนคำตอบสำเร็จในรูปแบบช่วงของ \(x\lt 0\) และ \(x\gt -1\)

เฉลย

อสมการพหุนามตัวแปรเดียว

หลังจากที่เรารู้เรื่องคำตอบของอสมการแล้ว เรามาดูกันว่าแก้การอสมการพหุนามตัวแปรเดียวทำได้ยังไงบ้าง (ดีกรีหนึ่งจะเรียก อสมการเชิงเส้นตัวแปรเดียว ที่เราเรียนตอน ม.3 ดังนั้น บทนี้จะเราจะโฟกัส ดีกรีสองขึ้นไปนะ)

ขั้นตอนแก้อสมการพหุนาม

จัดรูปให้ฝั่งนึงเป็น \(0\)
อีกฝั่งจัดรูปแยกตัวประกอบ ให้อยู่ในรูปเศษส่วนพหุนาม โดยที่เศษและส่วนแยกตัวประกอบเรียบร้อยแล้ว
กำจัดส่วน โดยการคูณด้วย กำลังสอง
แก้เครื่องหมาย ถ้ามีวงเล็บ \(-x\) โดยคูณ \(-1\) ตลอดสมการ
เขียนเส้นจำนวน และ หาคำตอบ

เดี๋ยวเราจะมาดูกันว่าขั้นตอนข้างบน ใช้จริงได้ยังไง สมมติเราต้องการแก้อสมการ \(x\gt\dfrac{12}{x}-1\)

ขั้นตอนที่ 1 ฝั่งขวาเป็น 0

เราทำคล้าย ๆ การแก้สมการพหุนามดีกรีสองขึ้นไปเลยครับ คือ จัดฝั่งนึงเป็น \(0\) จะได้ว่า

\(x-\dfrac{12}{x}+1\gt 0\)

ขั้นตอนที่ 2 จัดรูปเศษส่วนพหุนามและแยกตัวประกอบบนล่าง 0

บางคนชินกับการนำ \(x\) คูณตลอดทั้งสมการเพื่อให้ตัวส่วนไม่ติด \(x\) ขอบอกว่าช้าก่อน เพราะนี่คืออสมการ การนำ \(x\) คูณตลอด เราไม่รู้ว่า \(x\) เป็นบวกหรือลบ ยกเว้นโจทย์จะบอกมา ดังนั้น ข้อนี้โจทย์ไม่ได้บอกอะไรเพิ่ม \(x\) เป็นได้ทั้งบวกและลบ จะนำไปคูณตลอดสมการไม่ได้ เพราะเราไม่รู้ว่าจะต้องกลับเครื่องหมายหรือเปล่า นั่นเอง

ดังนั้น ข้อนี้เราจึงต้องจัดรูปฝั่งซ้ายเอา โดยการทำส่วนให้เป็น \(x\) เท่ากันได้ว่า

\(\require{cancel}\begin{aligned} \dfrac{x^2}{x}-\dfrac{12}{x}+\dfrac{x}{x}&\gt 0 \\\dfrac{x^2+x-12}{x}&\gt 0 \end{aligned}\)

จากนั้นเราก็ต้องแยกตัวประกอบ

\(\require{cancel}\begin{aligned} \dfrac{(x+4)(x-3)}{x}&\gt 0 \end{aligned}\)

ขั้นตอนที่ 3 กำลังสองของตัวส่วนคูณตลอด

หลักการที่เราจะทำ ถ้าติดตัวส่วน เราจะนำแต่ละวงเล็บของตัวส่วนยกกำลังสอง แล้วคูณตลอดสมการ เราคูณได้เพราะกำลังสองเป็นบวกเสมอดังนั้น ไม่ต้องกลับเครื่องหมาย แต่อย่าลืมใส่โน้ตไว้ว่า ตัวส่วนห้ามเป็นศูนย์

\(\require{cancel}\begin{aligned} \dfrac{x^2\cdot(x+4)(x-3)}{x}&\gt 0\cdot x^2 \\x(x+4)(x-3)&\gt 0\;\;,\;\; x\ne 0 \end{aligned}\)

สังเกตว่ามันก็เหมือนกับการย้ายตัวหารไปอยู่ข้างบนนั่นเอง

ขั้นตอนที่ 4 กำจัดพจน์ที่เครื่องหมายหน้า \(x\) เป็นลบ

สังเกตในข้อนี้เราไม่มี เราเลยไม่ต้องทำอะไร แต่ถ้ามีก็ให้นำ \(-1\) คูณตลอดและกลับเครื่องหมายด้วย

ขั้นตอนที่ 5 หาค่าวิกฤต (แต่ละวงเล็บ = 0) และเขียนเส้นจำนวนไล่ บวกลบบวก จากขวาสุด

จริง ๆ มันมีหลักการว่าทำไมต้องทำแบบนี้ พี่ขอยกไปพูดเพิ่มเติมไว้ให้ในวิดีโอ หากใครสนใจที่มา และหลักการ คิดโจทย์แบบไม่ต้องทำ ขั้นตอน 3 และ 4 ว่าต้องทำยังไงสามารถดูคลิปวิดีโอได้เลยนะครับ กล่าวง่าย ๆ คือ เมื่อเขียนเป็นอสมการแบบ ขั้นตอนที่ 2 (หลังแยกตัวประกอบ) เราสามารถเขียนเส้นจำนวนและหาคำตอบใน ขั้นตอนที่ 5 ได้เลย

\(\require{cancel} \begin{aligned} x(x+4)(x-3)\gt 0 \end{aligned}\)

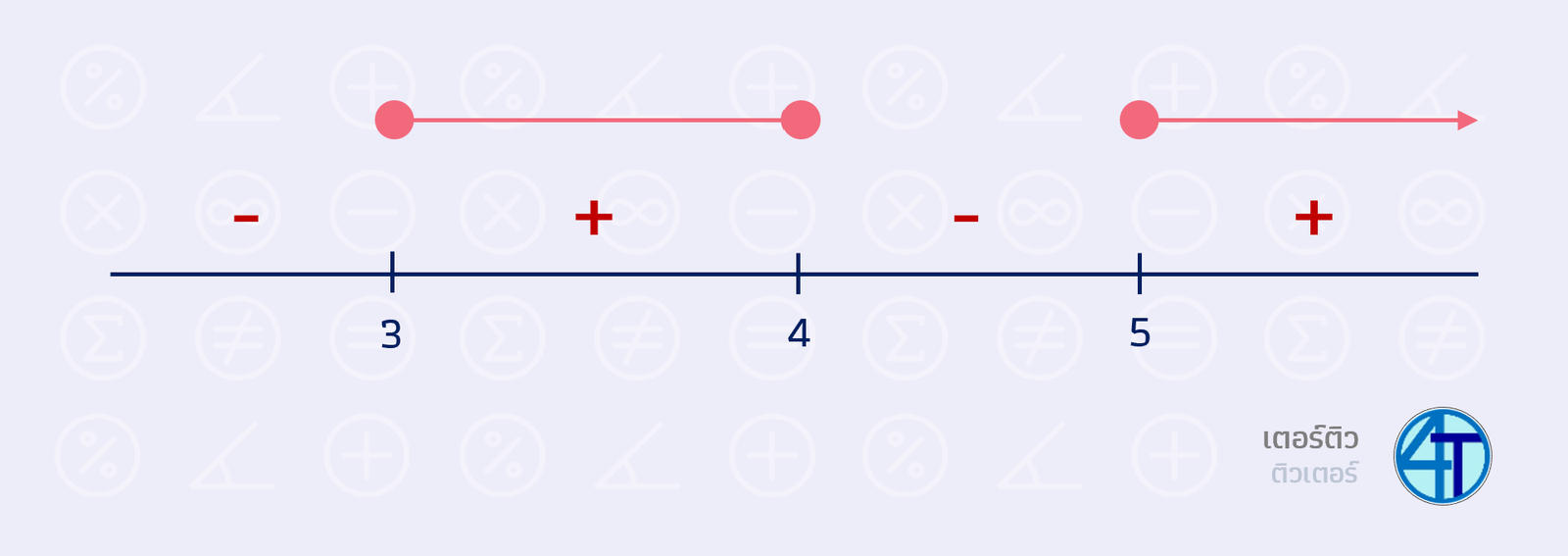
ค่าวิกฤตในข้อนี้ คือ \(0, -4, 3\) ดังนั้นเขียนเส้นจำนวนได้ ดังนี้ ใส่ บวกลบบวก สลับกันไปเรื่อย ๆ จากขวาไปซ้าย

การใส่เครื่องหมาย \(+,-,+\) ให้สลับเครื่องหมายเฉพาะ พจน์ยกกำลังเลขคี่ เท่านั้น ในตัวอย่างนี้ยกกำลัง 1 ทั้งหมด ดังนั้น สลับเครื่องทุกค่าวิกฤต

คำตอบเอาช่วงตามนี้

ถ้าอสมการเป็นเครื่องหมาย \(\gt 0\) เอาช่วงบวก (ค่าวิกฤตไม่เอา - ช่วงเปิด)
ถ้าอสมการเป็นเครื่องหมาย \(\ge 0\) เอาช่วงบวก (ค่าวิกฤตเอา - ช่วงปิด)
ถ้าอสมการเป็นเครื่องหมาย \(\lt 0\) เอาช่วงลบ (ค่าวิกฤตไม่เอา - ช่วงเปิด)
ถ้าอสมการเป็นเครื่องหมาย \(\le 0\) เอาช่วงลบ (ค่าวิกฤตเอา - ช่วงปิด)

ซึ่งข้อนี้ คือ \(\gt 0\) เอาช่วงบวกที่เป็นช่วงเปิด ดังนั้น เราจะได้ \((-4,0)\cup(3,\infty)\)

โดยเราโน้ตไว้ว่า \(x\ne 0\) ซึ่งคำตอบไม่มีอยู่แล้ว ก็ไม่ต้องตัดออก ดังนั้น ข้อนี้ตอบ \((-4,0)\cup(3, \infty)\)

คำแนะนำในการฝึกฝน เนื่องจากเรื่องนี้เน้นการฝึกฝน และอธิบายคอนเซปต์วิธีการแก้ยาก เพราะมีหลายเคสที่แปลก ๆ ดังนั้น พี่แนะนำให้น้องขั้นแรก ดูวิดีโอที่สอนเรื่องนี้ด้านบน และฝึกโจทย์ด้านล่างนี้ ลองทำเองดูก่อน และค่อยเปิดดูเฉลยว่ากระบวนการที่พี่คิด เป็นยังไง น่าจะช่วยให้น้อง ๆ แก้อสมการพหุนาม ได้เก่งมากขึ้นครับ

จงหาเซตของคำตอบของ \(\dfrac{(2x+1)(x-2)}{2-x}\ge0\)

เฉลย

เนื่องจากข้อนี้จัดรูปและแยกตัวประกอบให้แล้ว ดังนั้น ข้ามไปขั้นตอน 3 เราต้องกำจัดส่วนโดยคูณกำลังสองตลอดอสมการ

\(\require{cancel}\begin{aligned} (2-x)^2\cdot\dfrac{(2x+1)(x-2)}{2-x}&\ge (2-x)^2\cdot0 \\(2-x)(2x+1)(x-2)&\ge 0 \end{aligned}\)

อนาคตเราจะไม่ต้องเขียนขนาดนี้และ เราจะย้ายส่วนขึ้นไปได้เลย (รู้ว่าคูณกำลังสองในใจ) และจากนั้นก็จะโน้ตไว้ว่า ตัวส่วนไม่ใช่ \(0\) หรือ \(x\ne 2\) นั่นเอง

ขั้นตอน \(4\) เราจะคูณ \(-1\) ตลอดสมการเพื่อได้ปัญหาพจน์ \(2-x\) เพราะ \(x\) ติดลบ ได้ว่า

\(\require{cancel}\begin{aligned} (x-2)(2x+1)(x-2)&\le 0 \\(x-2)^2(2x+1)&\le 0 \end{aligned}\)

ขั้นตอนที่ 5 หาค่าวิกฤต ได้ว่า \(-\dfrac{1}{2}, 2\) และเขียนเครื่องหมาย \(+,-,+\) จากขวาไปซ้าย อย่าลืมว่าพจน์กำลังคู่ ไม่ต้องสลับเครื่องหมาย

ข้อนี้เครื่องหมายคือ \(\le 0\) ซึ่งคือเอาช่วงลบ (เอาค่าวิกฤตด้วย) จะได้ว่าคำตอบคือ \(\left(-\infty,-\dfrac{1}{2}\right]\cup\{2\}\) แต่เราโน้ตไว้ว่า \(x\ne 2\) ดังนั้น เลยได้ \(\left(-\infty, -\dfrac{1}{2}\right]\)

จงหาเซตของคำตอบของ \((x^2-2)(x^2+1)\le 10\)

เฉลย

ข้อนี้บางคนดีใจว่าโจทย์จัดรูปให้แล้ว แต่จริง ๆ ไม่ใช่เลยครับ เพราะถึงฝั่งซ้ายจะแยกตัวประกอบมาแล้ว ฝั่งขวายังไม่เป็น \(0\) ดังนั้น เราต้องกระจายกลับและนำ \(10\) ย้ายไปลบแล้วค่อยแยกตัวประกอบใหม่อีกที

\(\require{cancel}\begin{aligned} (x^2-2)(x^2+1)&\le 10 \\x^4-x^2-2&\le 10 \\x^4-x^2-12&\le 0 \\(x^2-4)(x^2+3)&\le 0 \end{aligned}\)

ใครงง ๆ การจัดรูปด้านบนลองแทน \(x^2\) เป็น \(A\) ก็ได้นะ แล้วค่อยแทนกลับคืน จะได้ไม่เป็นกำลังสี่

เมื่อเสร็จแล้วเราแยกต่อ วงเล็บซ้ายคือ ผลต่างกำลังสอง แต่วงเล็บขวาแยกต่อไม่ได้แล้ว

\(\require{cancel}\begin{aligned} (x-2)(x+2)(x^2+3)&\le 0 \end{aligned}\)

สังเกตถ้าเจอพจน์ประเภทนี้ \(x^2+3\) ให้เราดูว่ามัน \(\gt 0\) เสมอหรือเปล่า ถ้าใช่ ก็ย้ายไปหารได้เลย ซึ่ง \(x^2+3\gt 0\) ดังนั้น เราย้ายไปหารเพื่อตัดพจน์นี้ทิ้งได้ เพราะมันเป็นบวกและไม่ใช่ศูนย์ เราจึงหารได้โดยไม่ต้องกังวลเครื่องหมาย

\(\require{cancel}\begin{aligned} (x-2)(x+2)&\le \dfrac{0}{(x^2+3)} \\(x-2)(x+2)&\le 0 \end{aligned}\)

จบแล้ว ค่าวิกฤตคือ \(-2, 2\) ดังนั้น เขียนเส้นจำนวนและใส่ บวกลบบวก ได้ตามนี้

เราเอาช่วงลบ และข้อนี้มีเครื่องหมายเท่ากับ เพราะเป็น \(\le\) เราจึงเอาค่าวิกฤตด้วย ได้ว่า \([-2,2]\) เป็นคำตอบ

จงหาเซตของคำตอบของ \(25-9x^2\gt 0\)

เฉลย

จงหาเซตของคำตอบของ \(\dfrac{(x^2+5)(4-x)(5-x)}{(x-3)^3}\ge 0\)

เฉลย

ข้อนี้ฝึกความเข้าใจเพราะโจทย์แยกตัวประกอบมาให้หมดแล้ว ขั้นแรกเราต้องกำจัดตัวส่วน และโน้ตไว้ว่า \(x\ne 3\) หลักการกำจัดตัวส่วนก็คือยกมันขึ้นไปเลย อย่าไปสนใจยกกำลังมาก เพราะสุดท้ายไอเดียก็คือ คูณตัวมันยกกำลังสอง ก็คือคูณ \(((x-3)^3)^2\) ประมาณนี้

\(\require{cancel}\begin{aligned} (x-3)^3(x^2+5)(4-x)(5-x)\ge 0\;\;,\;\; x\ne 3 \end{aligned}\)

ต่อไปเราต้องจัดการ พจน์ที่ \(x\) ติดลบ ซึ่งข้อนี้มี 2 พจน์ เราก็จะคูณ \(-1\) ไปสองที และกระจายไปให้แต่ละตัว

\(\require{cancel}\begin{aligned} (-1)(-1)\cdot(x-3)^3(x^2+5)(4-x)(5-x)&\ge (-1)(-1)\cdot0 \\(x-3)^3(x^2+5)(-1)(4-x)(-1)(5-x)&\ge 0 \\(x-3)^3(x^2+5)(x-4)(x-5)&\ge 0 \end{aligned}\)

สังเกตว่าข้อนี้เครื่องหมายไม่กลับ เพราะจริง ๆ มันกลับสองที (เราคูณ -1 ไปสองตัว มันก็จะกลับ \(\ge\,\to\,\le\,\to\,\ge\)) ก็กลายเป็นตัวเดิม ดังนั้น จำไว้เสมอว่า

ถ้าต้องคูณ \(-1\) ไปคี่ตัว เราจะได้เครื่องหมายตรงข้าม ถ้าคูณ \(-1\) คู่ตัว จะได้เครื่องหมายเหมือนเดิม

พจน์ \(x^2+5\) เป็นบวกเสมอ ดังนั้น นำไปหารทิ้งได้เลย จะเหลือ

\(\require{cancel}\begin{aligned} (x-3)^3(x-4)(x-5)&\ge 0 \end{aligned}\)

ค่าวิกฤตมีดังนี้ \(3,4,5\) ซึ่งทั้งหมดเป็นยกกำลังคี่ ดังนั้น เครื่องหมายสลับ บวกลบบวก ตามปกติ

ข้อนี้เราเป็นเครื่องหมาย \(\ge 0\) ดังนั้น เอาช่วงบวกและก็เอาค่าวิกฤตด้วย ได้ว่า \([3,4]\cup[5,\infty)\) แต่ข้อนี้เราโน้ตไว้แล้วว่า \(x\ne 3\) ก็จะได้ว่า ไม่เอา \(3\) เลยต้องเป็นช่วงเปิดตรง \(3\) คำตอบคือ \((3,4]\cup[5,\infty)\)

จงหาเซตของคำตอบของ \(\dfrac{x}{x^2-4x+3}\le\dfrac{x+5}{x^2-1}\)

เฉลย

อย่าเผลอไปคูณไขว้เด็ดขาดนะ เพราะนี่คือเรื่องอสมการ ดังนั้น เราต้องย้ายไปลบแทน และจับส่วนเท่ากัน

\(\require{cancel}\begin{aligned} \dfrac{x}{x^2-4x+3}-\dfrac{x+5}{x^2-1}&\le 0 \\\dfrac{x}{(x-3)(x-1)}-\dfrac{x+5}{(x+1)(x-1)}&\le 0 \\\dfrac{x(x+1)}{(x-3)(x-1)(x+1)}-\dfrac{(x+5)(x-3)}{(x+1)(x-1)(x-3)}&\le 0 \\\dfrac{x(x+1)-(x+5)(x-3)}{(x-3)(x+1)(x-1)}&\le 0 \\\dfrac{15-x}{(x-3)(x+1)(x-1)}&\le 0 \end{aligned}\)

เมื่อได้แบบนี้ เราก็โยนตัวส่วนไปข้างบน (จริง ๆ คือคูณตัวมันยกกำลังสอง) และโน้ตว่าตัวส่วนไม่เป็น \(0\) หมายความว่า แต่ละวงเล็บไม่เป็น \(0\) คือ \(x\ne 3, x\ne \pm1\)

\(\require{cancel}\begin{aligned} (15-x)(x-3)(x+1)(x-1)&\le 0 \end{aligned}\)

จากนั้นนำ \(-1\) ไปคูณ 1 ทีแก้พจน์ติดลบ \(15-x\) ได้ว่า

\(\require{cancel}\begin{aligned} (x-15)(x-3)(x+1)(x-1)&\ge 0 \end{aligned}\)

ค่าวิกฤต คือ \(-1, 1, 3, 15\) และเราเอาช่วงบวก เพราะ \(\ge 0\) เอาค่าวิกฤตด้วย ได้ว่า

ได้ว่า \((-\infty, -1]\cup[1,3]\cup[15,\infty)\) แต่เราโน้ตไว้ว่า \(x\ne 3,x\ne \pm1\) ดังนั้น คำตอบคือ \((-\infty, -1)\cup(1,3)\cup[15,\infty)\)

หากบทความพี่เป็นประโยชน์ ฝากแชร์ต่อให้เพื่อนๆ ด้วยนะครับ :')