บทกลับของทฤษฎีบทพีทาโกรัส คณิตศาสตร์ ม.2

บทกลับทฤษฎีบทพีทาโกรัส

ตอนที่แล้ว เรารู้แล้วว่า (1) มีสามเหลี่ยมมุมฉาก (2) ใช้สูตรพีทาโกรัส เรื่องบทกลับเราก็จะทำกลับกันครับน้องๆ คือเราจะ (1) ใช้สูตรพีทาโกรัส (2) เพื่อหาว่า สามเหลี่ยมนั้นเป็นมุมฉากหรือเปล่า

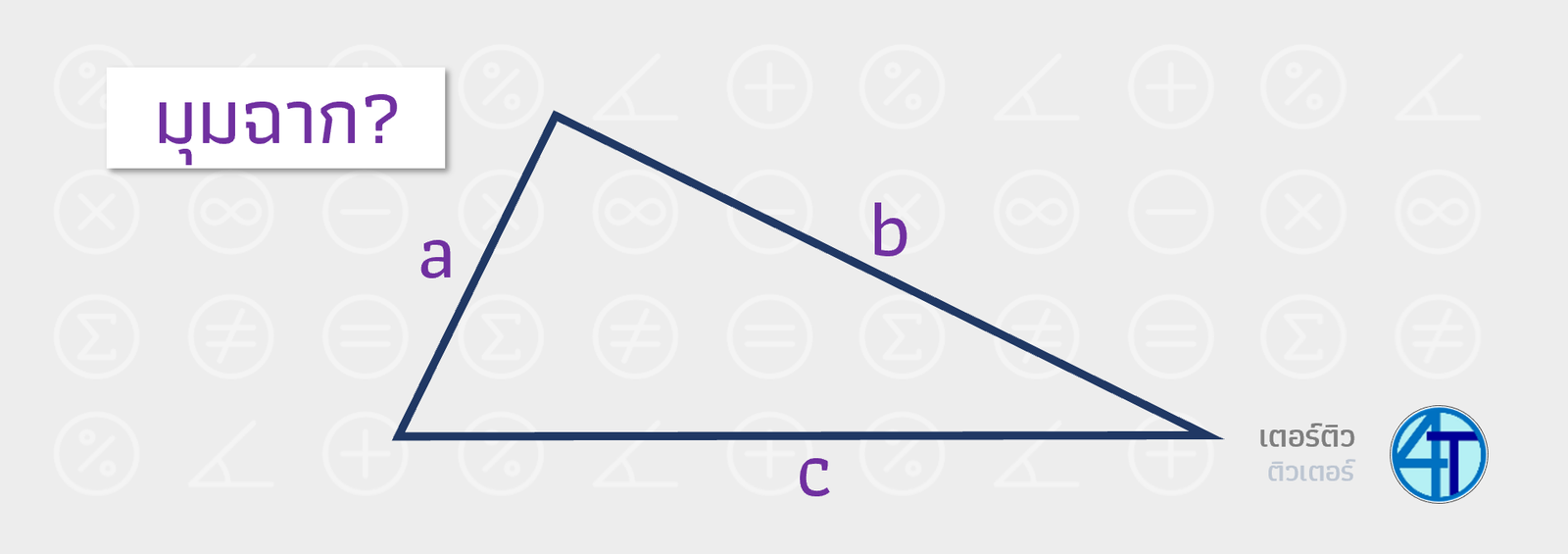
ก่อนอื่นเราต้องมองให้ออกก่อนว่า ด้านตรงข้ามมุมฉากนั้นเป็นด้านที่ยาวสุด ของสามเหลี่ยมมุมฉาก ดังนั้นหากน้องได้ความยาวด้านมา 3 ด้าน สมมติว่าคือ \(a,b,c\) โดยที่ \(a\lt b\lt c\) เราต้องจับด้านที่ยาวสุดเป็นค่า \(c\) ในสมการ \(a^2+b^2=c^2\) ส่วนด้านที่เหลือเราจะให้อันไหนเป็นค่า \(a\) หรือ \(b\) ก็ตามแต่ เพราะว่า การบวกกันสลับที่ได้

ตัวอย่างการใช้บทกลับทฤษฎีบทพีทาโกรัส

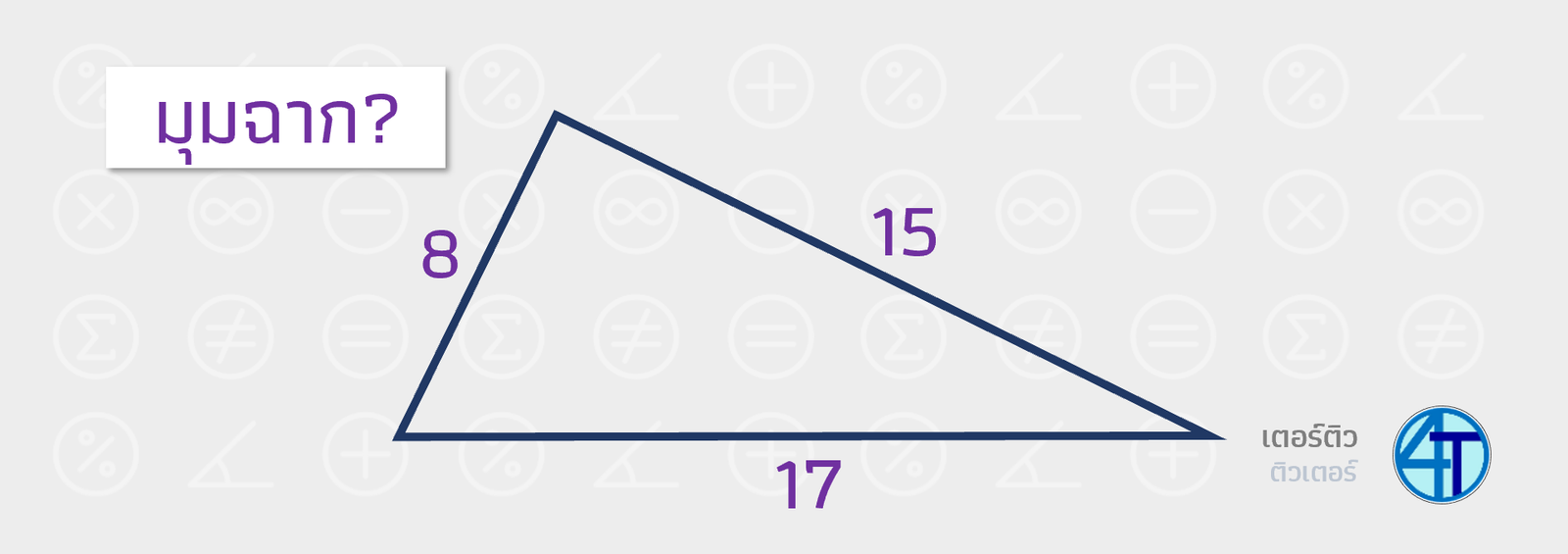
จากตัวอย่างข้างบนเรามีด้านสามด้านความยาว \(8,15,17\) ตามลำดับ เนื่องจาก \(17\) ยาวสุดเราจึงกำหนดให้ \(c=17\) และ \(a=8,b=15\) (ใครจะให้ \(a=15,b=8\) ก็ไม่ผิด)

เมื่อเราได้ค่าของตัวแปรแต่ละตัวแล้ว สิ่งที่เราต้องทำคือ แทนค่าในสมการพีทาโกรัส หากเป็นจริงก็แสดงว่ามันเป็นสามเหลี่ยมมุมฉากนั่นเอง \(a^2+b^2=\,8^2\,+\,15^2\,\)\(=64+225=\textcolor{red}{289}\) และ \(c^2=\,17^2\,=\textcolor{blue}{289}\) ซึ่งทั้งสองฝั่งนั้นมีค่าเท่ากัน ดังนั้นสามเหลี่ยมที่มีด้านยาว \(8,15,17\) เป็นสามเหลี่ยมมุมฉาก

สามเหลี่ยมมุมแหลม และ มุมป้าน

อันนี้เป็นผลพลอยได้ของสมการทฤษฎีบทพีทาโกรัส คือถ้าเราแทนสมการแล้ว \(a^2+b^2\neq c^2\) เราสามารถแบ่งมันออกเป็น 2 เคสด้วยกัน ได้แก่

เคสหนึ่ง \(c^2\gt a^2+b^2\) : ในเคสนี้หาก \(c\) ยาวกว่าที่จะทำให้เป็นมุมฉาก สามเหลี่ยมมันต้องโดนง้างมุมออกไปอีกถูกมั้ย ดังนั้นกรณีนี้จึงทำให้มุม \(\gt 90^{\circ}\) จึงเป็น สามเหลี่ยมมุมป้าน

เคสสอง \(c^2\lt a^2+b^2\) : ในทางกลับกันอันนี้ก็คือ สามเหลี่ยมมุมแหลม

แบบฝึกหัดประยุกต์บทกลับ

ในแต่ละข้อจงหาว่าสามเปลี่ยมที่ให้เป็นสามเหลี่ยมมุมฉากหรือไม่